
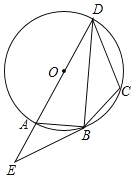
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接![]() ,证明
,证明![]() ,可得
,可得![]() ,则
,则![]() ;
;
(2)证明![]() ,
,![]() ,则
,则![]() ,可求出
,可求出![]() ,则答案可求出.
,则答案可求出.
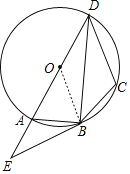
解:(1)证明:连接OB,
∵BE为⊙O的切线,
∴OB⊥BE,
∴∠OBE=90°,
∴∠ABE+∠OBA=90°,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠ABE+∠OAB=90°,
∵AD是⊙O的直径,
∴∠OAB+∠ADB=90°,
∴∠ABE=∠ADB,
∵四边形ABCD的外接圆为⊙O,
∴∠EAB=∠C,
∵∠E=∠DBC,
∴∠ABE=∠BDC,
∴∠ADB=∠BDC,
即DB平分∠ADC;
(2)解:∵tan∠ABE=![]() ,
,
∴设AB=x,则BD=2x,
AD=![]() =
=![]() x,
x,
∵∠E=∠E,∠ABE=∠BDE,
∴△AEB∽△BED,
∴BE2=AEDE,且![]() =
=![]() =
=![]() ,
,
设AE=a,则BE=2a,
∴4a2=a(a+![]() x),
x),
∴a=![]() x,
x,
∵∠BAE=∠C,∠ABE=∠BDC,
<>∴△AEB∽△CBD,∴![]() ,
,
∴![]() =
=![]() ,
,
解得=3![]() ,
,
∴AD=![]() x=15,
x=15,
∴OA=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
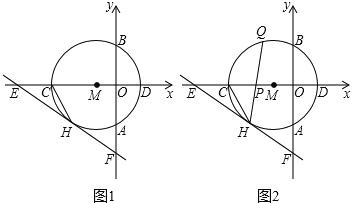
【题目】如图1所示,以点M(1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E(![]() ,0),交y轴于点F(0,
,0),交y轴于点F(0,![]() ).
).
(1)求⊙M的半径r;
(2)如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC=![]() ,求
,求![]() 的值;
的值;
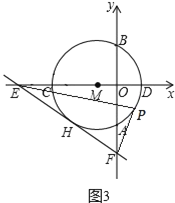
(3)如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+![]() PE的最小值.
PE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相
交于点E,且AE平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠EAB=30°,OD=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
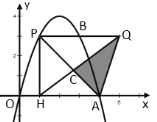
【题目】如图,抛物线![]() 上有一点
上有一点![]() ,
,![]() 的横坐标为1,过
的横坐标为1,过![]() 作
作![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,且
,且![]() ,作
,作![]() 轴,垂足为
轴,垂足为![]() ,抛物线与
,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连结
,连结![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)当![]() 时,①求点
时,①求点![]() 的坐标:②求
的坐标:②求![]() 的面积:
的面积:
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
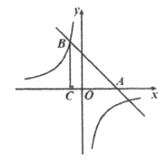
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点P为AD上一个动点,以PB 为对称轴将△APB折叠得到△EPB,点A的对称点为点E,射线BE交矩形ABCD的边于点 F,若AB=4,AD=6,当点F为矩形ABCD边的中点时,AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com