
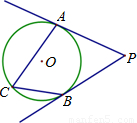
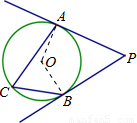
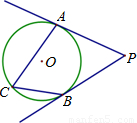
 解:连接OA、OB,
解:连接OA、OB,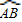 所对的圆周角和圆心角,
所对的圆周角和圆心角, ∠AOB=
∠AOB= ×110°=55°.
×110°=55°.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
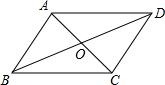 如图所示,?ABCD的两条对角线相交于点O,OA,OB,AB的长分别为5cm,13cm,12cm,则CD=
如图所示,?ABCD的两条对角线相交于点O,OA,OB,AB的长分别为5cm,13cm,12cm,则CD=查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
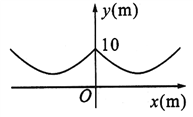
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称。
(1)钢缆最低点到桥面的距离是多少?
(2)两条钢缆的最低点之间的距离是多少?
(3)写出右边钢缆抛物线的解析式。
查看答案和解析>>
科目:初中数学 来源:2011年青海省中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com