

 :2
:2 :3
:3 ×高×底,所以相似三角形的面积之比等于边之比的平方,由DE⊥AC,EF⊥AB,FC⊥BC得出△DEF与△ABC的角对应相等,即:△DEF∽△CAB,求出两个三角形的边之比即可,又知△ABC是正三角形,所以∠B=∠C=∠A=60°,利用余弦和正弦定理求出两个三角形的边之比.
×高×底,所以相似三角形的面积之比等于边之比的平方,由DE⊥AC,EF⊥AB,FC⊥BC得出△DEF与△ABC的角对应相等,即:△DEF∽△CAB,求出两个三角形的边之比即可,又知△ABC是正三角形,所以∠B=∠C=∠A=60°,利用余弦和正弦定理求出两个三角形的边之比.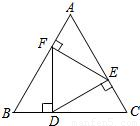 ,
,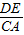 )2,
)2,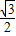 DC,EC=cos∠C×DC=
DC,EC=cos∠C×DC= DC,
DC, DC,
DC,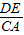 =
=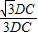 =
=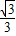 ,
,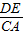 )2=
)2= =1:3.
=1:3.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2009年浙江省湖州市中考数学试卷(解析版) 题型:选择题

 :2
:2 :3
:3查看答案和解析>>
科目:初中数学 来源:2009年浙江省湖州市中考数学试卷(解析版) 题型:选择题
 (2009•湖州)如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
(2009•湖州)如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )



查看答案和解析>>
科目:初中数学 来源:2009年广东省深圳市中考数学试卷(模拟)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com