
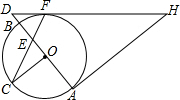
 如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D.
如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D.分析 (1)连结OF,如图,由切线性质得∠1+∠2=90°,再由OC⊥AB得∠C+∠4=90°,然后利用等量代换得到∠1=∠3,则根据等腰三角形的判定定理即可得到结论;
(2)在Rt△OEC中利用正切定义求出OE=$\frac{1}{2}$OC=2,设DF=x,则DE=x,根据勾股定理得到x2+42=(x+2)2,解得x=3,再利用切线长定理和切线性质得到HF=HA,DA⊥AH,设AH=t,则HF=t,则根据勾股定理得到t2+92=(t+3)2,然后解方程即可.
解答 (1)证明:连结OF,如图,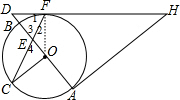
∵DH为切线,
∴OF⊥DH,
∴∠1+∠2=90°,
∵OC⊥AB,
∴∠C+∠4=90°,
∵OF=OC,
∴∠2=∠C,
而∠3=∠4,
∴∠1=∠3,
∴DE=DF;
(2)解:在Rt△OEC中,∵tan∠OCE=$\frac{OE}{OC}$,
∴OE=$\frac{1}{2}$OC=2,
设DF=x,则DE=x,
在Rt△OFD中,x2+42=(x+2)2,解得x=3,
∴DF=3,DO=5,
∵HF和HA为切线,
∴HF=HA,DA⊥AH,
设AH=t,则HF=t,
在Rt△DAH中,t2+92=(t+3)2,解得t=12,
即AH的长为12.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.灵活应用勾股定理是解决(2)小题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 调查奥运会金牌获得者的兴奋剂使用情况 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
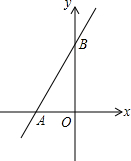 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
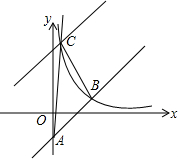 如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).
如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com