
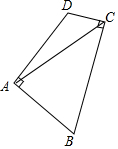
 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18.
如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18. 分析 作辅助线;证明△ABM≌△ADN,得到AM=AN,△ABM与△ADN的面积相等;求出正方形AMCN的面积即可解决问题.
解答 解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N;
∵∠BAD=∠BCD=90°
∴四边形AMCN为矩形,∠MAN=90°;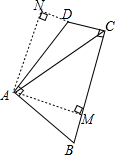
∵∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
$\left\{\begin{array}{l}{∠BAM=∠DAN}\\{∠AMB=∠AND}\\{AB=AD}\end{array}\right.$,
∴△ABM≌△ADN(AAS),
∴AM=AN(设为λ);△ABM与△ADN的面积相等;
∴四边形ABCD的面积=正方形AMCN的面积;
由勾股定理得:AC2=AM2+MC2,而AC=6;
∴2λ2=36,λ2=18,
故答案为:18.
点评 本题主要考查了全等三角形的判定及其性质、正方形的判定及其性质等几何知识点的应用问题;解题的关键是作辅助线,构造全等三角形和正方形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
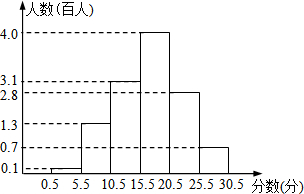 2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:
2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
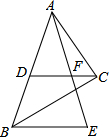 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )| A. | 6 | B. | 4 | C. | 7 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
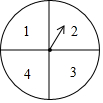 由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
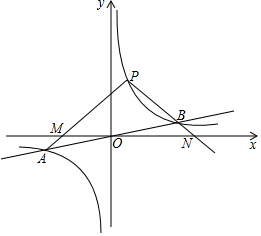 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
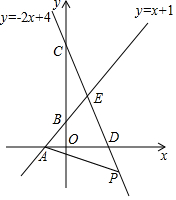 如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x、y轴交于点D,C,这两条直线交于点E.
如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x、y轴交于点D,C,这两条直线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
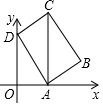 如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴.
如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从数轴的原点O向右数出3个单位,记为点A,过点A作数轴的垂线并截取AB为1个单位长度,连接OB,以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C所表示的实数为$\sqrt{10}$.
如图,从数轴的原点O向右数出3个单位,记为点A,过点A作数轴的垂线并截取AB为1个单位长度,连接OB,以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C所表示的实数为$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com