练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
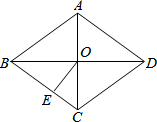
    7．如图，菱形ABCD的面积为S，对角线交于点O，OE⊥BC于点E．下列结论正确的是（　　）
    A．S=AC•BDB．S=4BC•OEC．S=2AB•OED．S=2BD•AO

    分析 由ABCD是菱形，推出AB=BC，由于菱形的对角线把菱形分成4个全等的直角三角形，根据三角形的面积公式可求出结论．

    解答 解：∵ABCD是菱形，
    ∴AB=BC，
    ∴S=4S△OBC=4×$\frac{1}{2}$BC•OE=2AB•OE，
    故选C．

    点评 本题主要考查了菱形的性质可三角形的面积公式，熟练掌握菱形的性质是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．我市为了鼓励居民节约用水，对居民生活用水的收费实行阶梯式计量水价的方法，具体规定如下：
     各阶梯 月用水量 基本水价（元、立方米）
     第一阶梯 不超过28立方米的部分 2
     第二阶梯 超过28立方米且不超过40立方米的部分 2.5
     第三阶梯 超过40立方米的部分 3
    设某户每月用水量为x立方米，应收水费y元
    （1）分别写出每月用水量在三个不同阶梯时，y与x的函数关系式．
    （2）已知小明家4月份缴纳水费83元，则他家该月共用水多少立方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连接EF．延长CD至G，使GD=EB，连接AG，易证△AFG≌△AFE．所以EF，BE，DF之间的数量关系为 EF=DF+BE．
    （1）如图2，点E，F分别在正方形ABCD的边BC，CD的延长线上，∠EAF=45°，连接EF．试猜想EF，BE，DF之间的数量关系；（直接写出结果，不需证明）
    （2）如图3，点E，F分别在正方形ABCD的边CB，DC的延长线上，∠EAF=45°，连接EF．试猜想EF，BE，DF之间的数量关系，并加以证明；
    （3）如图4，点E，F在正方形ABCD的对角线BD上，∠EAF=45°，若BE=2，DF=1，请直接写出EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

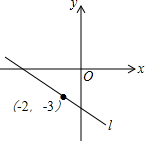    15．如图的坐标平面上，有一条通过点（-2，-3）的直线l．若四点（-2，a）、（0，b）、（c，0）、（d，-1）在l上，则下列数值判断正确是（　　）
    A．a=2B．b＞-3C．c＜-2D．d=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．刘俊问王老师的年龄时，王老师说：“我像你这么大时，你才3岁；等你到了我这么大时，我就45岁了．”设王老师今年x岁，刘俊今年y岁，根据题意，列方程组正确的是（　　）
    A．$\left\{\begin{array}{l}x-y=y+3\\ x-y=45+x\end{array}\right.$B．$\left\{\begin{array}{l}x-y=y+3\\ x-y=45-x\end{array}\right.$
    C．$\left\{\begin{array}{l}x-y=y-3\\ x-y=45+x\end{array}\right.$D．$\left\{\begin{array}{l}x-y=y-3\\ x-y=45-x\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．一根蜡烛高20cm，蜡烛高度 y（单位：cm）随燃烧的时间x（单位：分钟）的增加而减少，平均每分钟减少量为0.1cm/分钟．求y与x的函数关系式，并画出该函数的图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图1，已知矩形ABCD的对角线相交于点O，EF过点O分别交AB、CD于点E、F．
    （1）求证：△AOE≌△COF；
    （2）若AB=3，AD=4，点M在线段BC上运动，连接MO．
    ①当MO⊥AC时，求BM的值；
    ②当BM为多少时，△BMO是等腰三角形？（只写出结论，不要求写过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

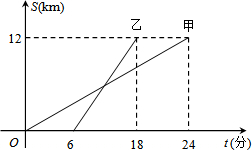    16．如图，表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．甲、乙两人前往目的地所行驶的路程S（千米）随时间t（分）变化的函数图象，则每分钟乙比甲多行驶的路程是（　　）
    A．0.5千米B．1千米C．1.5千米D．2千米

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列方程有两个相等的实数根的是（　　）
    A．x2+x+1=0B．4x2+2x+1=0C．x2+12x+36=0D．x2+x-2=0

    查看答案和解析>>

    同步练习册答案