
 2014��3��8���賿2��40�֣��������Ǻ��չ�˾��һ������239�˵IJ���777-200�ɻ����������ʧȥ��ϵ���ҹ���Ԯ�������Ͽ�չ�Ѿȹ�����һ���Ѿȴ���ij������8����A���������Ϸ�����һ������B����ͼ������ʱ��ô��͵������60$\sqrt{2}$�������ÿСʱ30������ٶ�����ƫ��24��ķ����е�C������ʱ���������ڴ����������ο����ݣ�sin24���0.4��cos24���0.9����
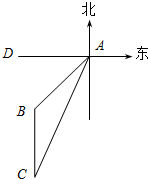
2014��3��8���賿2��40�֣��������Ǻ��չ�˾��һ������239�˵IJ���777-200�ɻ����������ʧȥ��ϵ���ҹ���Ԯ�������Ͽ�չ�Ѿȹ�����һ���Ѿȴ���ij������8����A���������Ϸ�����һ������B����ͼ������ʱ��ô��͵������60$\sqrt{2}$�������ÿСʱ30������ٶ�����ƫ��24��ķ����е�C������ʱ���������ڴ����������ο����ݣ�sin24���0.4��cos24���0.9�������� ��1��Ҫ�㵽��C������Ҫ�����AC�ľ��룬����ʱ��=��������ٶȣ��Ӷ�����⣮
��2�����͵����ľ������BC�ij�������CB���ӳ��߽�AD��E������ֱ�������εĽǣ������Ǻ��������BC�ij���
���  �⣺��1���ӳ�CB��AD���ڵ�E�����AEB=90�㣬
�⣺��1���ӳ�CB��AD���ڵ�E�����AEB=90�㣬
�ߡ�BAE=45�㣬AB=60$\sqrt{2}$��
��BE=AE=60��
��������ã���C=24�㣬
sin24��=$\frac{AE}{AC}$��
��AC=150��
150��30=5��
����13�㵽��C����
��2����ֱ��������ACE�У�cos24��=$\frac{EC}{AC}$��
��cos24��=$\frac{60+BC}{150}$��
BC=75��
���Դ���C��ʱ�����͵����ľ�����75���
���� ���⿼���˽�ֱ�������ε�Ӧ��-��������⣬�ؼ��������Ϸ�����������Ӷ��ҳ��ǵĶ��������������߹���ֱ�������δӶ�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC��
��ͼ����֪��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��-3�� | B�� | ��-3��1�� | C�� | ��1��3�� | D�� | ��-3��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
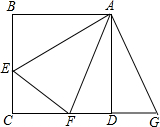 ������ABCD�У�E��F�ֱ��DZ�BC��CD�ϵĵ㣬�ҡ�EAF=45�㣬����ABE�Ƶ�A��ʱ����ת90�㣬�õ���ADG����֤��EF=BE+DF��
������ABCD�У�E��F�ֱ��DZ�BC��CD�ϵĵ㣬�ҡ�EAF=45�㣬����ABE�Ƶ�A��ʱ����ת90�㣬�õ���ADG����֤��EF=BE+DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com