
【题目】在Rt△ABC中,∠BAC=90,D是BC的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点F
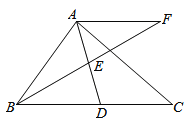
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积。
【答案】(1)证明见解析;(2)证明见解析;(3)10.
【解析】
试题分析:(1)根据AAS证明即可判定.
(2)先证明四边形ADCF是平行四边形,再证明DA=DC即可.
(3)利用S菱形ADCF=2S△ADC=S△ABC即可求解.
试题解析:(1)∵AF∥BD,
∴∠AFE=∠DBE,
∵E是AD中点,
∴AE=ED,
在△BDE和△FAE中,
 ,
,
∴△AFE≌△DBE.
(2)连接CF.

∵△AFE≌△DBE,
∴AF=BD
∵∠BAC=90°,BD=CD,
∴AD=DC=DB,
∴AF∥CD,AF=DC,
∴四边形ADCF是平行四边形,
∵DA=CD,
∴四边形ADCF是菱形.
(3)∵S△ABC=![]() ×AB×AC=10,
×AB×AC=10,
∵四边形ADCF是菱形,BD=DC,S△ABC=2S△ADC,
∴S菱形ADCF=2S△ADC=10.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+![]() =0.
=0.

(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果![]() =
=![]() ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1,S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1,S2(S1>S2)的两部分,如果![]() =
=![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
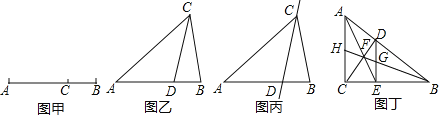
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-4,![]() ),B(-1,2)是一次函数y=kx+b的图像与反比例函数
),B(-1,2)是一次函数y=kx+b的图像与反比例函数![]() (m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
(m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
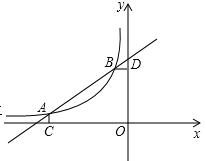
(1)根据函数图像直接回答问题:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数的表达式及m的值;
(3)点P是线段AB上一点,连接PC,PD,若△PCA和△PBD的面积相等,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com