
| A. | 2+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | 2-$\sqrt{3}$ |
分析 根据题意列出算式,利用二次根式乘法法则及平方差公式化简,计算即可得到结果.
解答 解:$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{3}}}}$•$\sqrt{2+\sqrt{2-\sqrt{2-\sqrt{3}}}}$•$\sqrt{2-\sqrt{2-\sqrt{3}}}$•$\sqrt{2-\sqrt{3}}$
=$\sqrt{(2-\sqrt{2-\sqrt{2-\sqrt{3}}})(2+\sqrt{2-\sqrt{2-\sqrt{3}}})}$•$\sqrt{2-\sqrt{2-\sqrt{3}}}$•$\sqrt{2-\sqrt{3}}$
=$\sqrt{2+\sqrt{2-\sqrt{3}}}$•$\sqrt{2-\sqrt{2-\sqrt{3}}}$•$\sqrt{2-\sqrt{3}}$
=$\sqrt{2+\sqrt{3}}$•$\sqrt{2-\sqrt{3}}$
=$\sqrt{4-3}$
=1.
故选C
点评 此题考查了实数的运算,以及平方差公式,熟练掌握公式及法则是解本题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
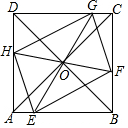 如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.
如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
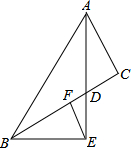 如图,△ABC中,AD是角平分线,BE⊥AD,垂足E在AD延长线上,F是BC的中点,AB=30cm,AC=18cm.则EF的长为6cm.
如图,△ABC中,AD是角平分线,BE⊥AD,垂足E在AD延长线上,F是BC的中点,AB=30cm,AC=18cm.则EF的长为6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com