
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表给出了以下结论:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
①二次函数y=ax2+bx+c有最小值,最小值为﹣3;②当﹣![]() <x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
<x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】
利用x=﹣1和x=3时函数值都为0可判断抛物线与x轴有两个交点坐标为(﹣1,0),(3,0),则可对③进行判断;利用表中数据得到当﹣1<x<3时,y<0,则可对②进行判断;利用对称性得到抛物线的对称轴为直线x=1,则可对①进行判断;根据二次函数的性质可对④进行判断.
∵x=﹣1和x=3时,y=0,
∴抛物线与x轴有两个交点坐标为(﹣1,0),(3,0),所以③正确;
∴当﹣1<x<3时,y<0,所以②错误;
∵点(﹣1,0)与(3,0)为抛物线上的对称点,
∴抛物线的对称轴为直线x=1,
∴当x=1时,二次函数有最小值﹣4,所以①错误;
∵抛物线开口向上,
∴当x<1时,y随x的增大而减小,所以④正确.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
查看答案和解析>>
科目:初中数学 来源: 题型:
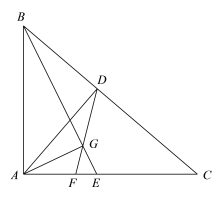
【题目】如图,△ABC中,D是BC上一点,E是AC上一点,点G在BE上,联结DG并延长交AE于点F,∠BGD=∠BAD=∠C.
(1)求证:![]() ;
;
(2)如果∠BAC=90°,求证:AG⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
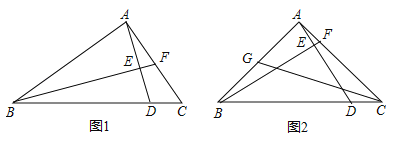
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
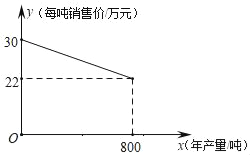
【题目】已知京润生物制品厂生产某种产品的年产量不超过800吨,生产该产品每吨所需相关费为10万元,且生产出的产品都能在当年销售完.产品每吨售价y(万元)与年产量x(吨)之间的函数关系如图所示
(1)当该产品年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣相关费用)
(2)当该产品年产量为多少吨时,该厂能获得当年销售的是大毛利润?最大毛利润多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
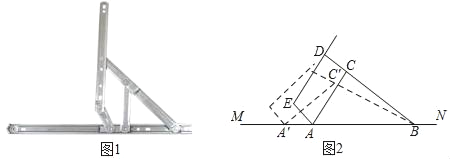
【题目】“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.
(1)求支点D到滑轨MN的距离(精确到1厘米);
(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,
≈2.45,![]() ≈2.65)
≈2.65)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0)、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,对称轴为直线x=1,交x轴于点E,tan∠BDE=![]() .
.
(1)求抛物线的表达式;
(2)若点P是对称轴上一点,且∠DCP=∠BDE,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=4,BC=5,CA=6.
(1)如果DE=10,那么当EF=________,FD=________时,△DEF∽△ABC;
(2)如果DE=10,那么当EF=________,FD=________时,△FDE∽△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com