练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
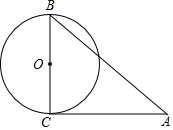
    11．如图，⊙O半径为4，BC是直径，AC是⊙O的切线，且AC=6，那么AB=（　　）
    A．4B．6C．10D．12

    分析 在Rt△ACB中，利用勾股定理计算即可解决问题．

    解答 解：∵AC是⊙O的切线，
    ∴AC⊥BC，
    ∴∠ACB=90°，
    ∵BC=8，AC=6，
    ∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10，
    故选C．

    点评 本题考查切线的性质、勾股定理等知识，解题的关键是掌握基本概念，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿，两家鸡腿的价格相同，品质相近．快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿．检查人员从两家的鸡腿中各随机抽取15个，记录它们的质量（单位：g）如表所示．
    质量（g）737475767778
    甲的数量244311
    乙的数量236211
    根据表中数据，回答下列问题：
    （1）甲厂抽取质量的中位数是75g；乙厂抽取质量的众数是75g．
    （2）如果快餐公司决定从平均数和方差两方面考虑选购，现已知抽取乙厂的样本平均数$\overline{x}$乙=75，方差S${\;}_{乙}^{2}$≈1.86．请你帮助计算出抽取甲厂的样本平均数及方差（结果保留小数点后两位），并指出快餐公司应选购哪家加工厂的鸡腿？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．【探究证明】
    （1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．
    如图1，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，求证：$\frac{EF}{GH}=\frac{AD}{AB}$；
    【结论应用】
    （2）如图2，在满足（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若$\frac{EF}{GH}=\frac{13}{17}$，则$\frac{BN}{AM}$的值为$\frac{13}{17}$；（直接写出结果）
    【联系拓展】
    （3）如图3，四边形ABCD中，∠ABC=90°，AB=AD=6，BC=CD=3，AM⊥DN，点M，N分别在边BC，AB上，求$\frac{DN}{AM}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．有一个周长80米的长方形花坛，长与宽的比是3：2．请用1：1000的比例尺画在图纸上，长和宽各应画多少厘米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．若|a-2|+（b+3）2=0，则（a+b）2008的值是（　　）
    A．0B．1C．-1D．2008

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

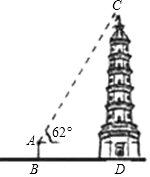    16．如图所示，位于昆明市昙华市内的瑞应塔，被誉为云南第一塔，某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度，甲同学在距离塔底部25m的B处地塔顶C的仰角为62°，若甲同学的眼睛到地面的高度AB为176cm，求瑞应塔C的高度（结果精确到0.1m，参考数据sin62°≈0.88，cos62°≈0.47，tan62°≈1.88）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：$\sqrt{9}$-（$\sqrt{2}$+$\sqrt{3}$）0+tan60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，①，A（4，0），C（0，n）分别是x和y轴上的点，n＞0，以OA，OC为边在第一象限内作矩形OABC，对角线OB，AC，交于点D双曲线y=$\frac{k}{x}$（x＞0，k＞0）交边BC于G，交边AB于H．
    （1）设直线AC的函数关系式为y=qx+p，请用含n的代数式表示q和p；
    （2）求证：AB•BG=BC•BH；
    （3）如图②，若上述双曲线经过点D，判断点D是否是双曲线与直线AC唯一的交点，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

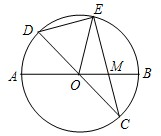    1． 已知：如图，在半径我4的⊙O中，AB、CD是两条直径，M我OB的中点，CM的延长线交⊙O于点E，且EM＞MC，连接DE，DE=$\sqrt{15}$．
    （1）求证：△AMC∽△EMB；
    （2）求EM的长；
    （3）求sin∠EOB的值．

    查看答案和解析>>

    同步练习册答案