
ЁОЬтФПЁПвбжЊЃЌШчЭМХзЮяЯпyЃНax2+3ax+cЃЈaЃО0ЃЉгыyжсНЛгкЕуCЃЌгыxжсНЛгкAЃЌBСНЕуЃЌЕуAдкЕуBзѓВрЃЎЕуBЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎOCЃН3OBЃЎ
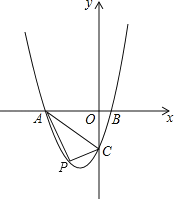
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЧѓШ§НЧаЮPACУцЛ§ЕФзюДѓжЕЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЁїPACЕФУцЛ§ЮЊSЃЌЦфжаSЮЊећЪ§ЕФЕуPзїЁАКУЕуЁБЃЌдђДцдкЖрИіЁАКУЕуЁБЃЌдђЫљгаЁАКУЕуЁБЕФИіЪ§ЮЊЁЁ ЁЁ
ЃЈ4ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌвдPAЮЊБпЯђжБЯпACгвЩЯВрзїе§ЗНаЮAPHGЃЌЫцзХЕуPЕФдЫЖЏЃЌе§ЗНаЮЕФДѓаЁЁЂЮЛжУвВЫцжЎИФБфЃЌЕБЖЅЕуHЛђGЧЁКУТфдкyжсЩЯЪБЃЌжБНгаДГіЖдгІЕФЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФБэДяЪНЮЊЃКyЃН![]() x2+
x2+![]() xЉ6ЃЛ
xЉ6ЃЛ
ЃЈ2ЃЉЕБxЃНЉ![]() ЪБЃЌSЕФзюДѓжЕЮЊЃК
ЪБЃЌSЕФзюДѓжЕЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ4ЃЛ
ЃЈ4ЃЉЕуPЕФзјБъЮЊЃКЃЈ![]() ЃЌЉ5ЃЉЛђЃЈ
ЃЌЉ5ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШШЗЖЈЕуCЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтЃЛ
ЃЈ2ЃЉЯШЧѓГіжБЯпACЕФНтЮіЪНЃЌдйЙ§ЕуPзїyжсЕФЦНааЯпНЛACгкЕуHЃЌЩшЕуPЕФКсзјБъЮЊxЃЌгЩгкЁїPACУцЛ§SЃН![]() PHЁСOAЃЌЧвOAвзЧѓЃЌжЛашгУКЌxЕФДњЪ§ЪНБэЪОГіPHЕФГЄМДПЩРћгУЖўДЮКЏЪ§ЕФаджЪЧѓГіНсЙћЃЛ
PHЁСOAЃЌЧвOAвзЧѓЃЌжЛашгУКЌxЕФДњЪ§ЪНБэЪОГіPHЕФГЄМДПЩРћгУЖўДЮКЏЪ§ЕФаджЪЧѓГіНсЙћЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЬтЕФЙиЯЕЪНВЂНсКЯxЕФЗЖЮЇж№вЛбщжЄSЪЧЗёЮЊећЪ§МДЕУД№АИЃЛ
ЃЈ4ЃЉЗжЕуGдкyжсЩЯКЭЕуHдкyжсЩЯСНжжЧщПіЃЌРћгУе§ЗНаЮЕФаджЪЙЙдьШЋЕШШ§НЧаЮЗжБ№ЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉOCЃН3OBЃН6ЃЌЙЪЕуBЁЂCЕФзјБъЗжБ№ЮЊЃКЃЈ2ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ6ЃЉЃЌдђХзЮяЯпЮЊyЃНax2+3axЉ6ЃЌ
НЋЕуBЕФзјБъДњШыЩЯЪНЕУЃК0ЃН4a+6aЉ6ЃЌНтЕУЃКaЃН![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЕФБэДяЪНЮЊЃКyЃН![]() x2+
x2+![]() xЉ6ЃЛ
xЉ6ЃЛ
ЃЈ2ЃЉyЃН![]() x2+
x2+![]() xЉ6ЃЌСюyЃН0ЃЌдђxЃНЉ5Лђ2ЃЌЙЪЕуAЃЈЉ5ЃЌ0ЃЉЃЌ
xЉ6ЃЌСюyЃН0ЃЌдђxЃНЉ5Лђ2ЃЌЙЪЕуAЃЈЉ5ЃЌ0ЃЉЃЌ
НЋЕуAЁЂCЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНЃКyЃНkx+bВЂНтЕУЃКжБЯпACЕФНтЮіЪНЮЊЃКyЃНЉ![]() xЉ6ЃЌ
xЉ6ЃЌ
Й§ЕуPзїyжсЕФЦНааЯпНЛACгкЕуHЃЌ

ЩшЕуPЃЈxЃЌ![]() x2+
x2+![]() xЉ6ЃЉЃЌЕуHЃЈxЃЌЉ
xЉ6ЃЉЃЌЕуHЃЈxЃЌЉ![]() xЉ6ЃЉЃЌ
xЉ6ЃЉЃЌ
ЁїPACУцЛ§SЃН![]() PHЁСOAЃН
PHЁСOAЃН![]() ЃНЉ
ЃНЉ![]() x2Љ
x2Љ![]() x
x![]() ЃЌ
ЃЌ
ЁпЉ![]() <0ЃЌЙЪSгазюДѓжЕЃЌ ЕБxЃНЉ
<0ЃЌЙЪSгазюДѓжЕЃЌ ЕБxЃНЉ![]() ЪБЃЌSЕФзюДѓжЕЮЊЃК
ЪБЃЌSЕФзюДѓжЕЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁїPACУцЛ§SЃНЉ![]() x2Љ
x2Љ![]() xЃЌвђЮЊЕуPЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЕуЃЌЫљвдЃ5<x<0ЃЌ
xЃЌвђЮЊЕуPЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЕуЃЌЫљвдЃ5<x<0ЃЌ
ЕБxЃНЉ4ЪБЃЌSЃН6ЃЛЕБxЃНЉ3ЪБЃЌsЃН9ЃЛЕБxЃНЉ2ЪБЃЌS=9ЃЛЕБxЃНЉ1ЪБЃЌsЃН6ЃЛ
ЫљвдЁАКУЕуЁБЕФИіЪ§ЮЊ4ЃЌ
ЙЪД№АИЮЊ4ЃЛ
ЃЈ4ЃЉШчЭМ2зѓВрЭМЃЌ
ЂйЕБЕуGдкyжсЩЯЪБЃЌзїPRЁЭxжсгкЕуRЃЌ
ЁпЁЯGAO+ЁЯPAOЃН90ЁуЃЌЁЯPAO+ЁЯAPRЃН90ЁуЃЌ
ЁрЁЯAPRЃНЁЯGAOЃЌ
ЁпЁЯAOGЃНЁЯPRAЃН90ЁуЃЌAPЃНAGЃЌ
ЁрЁїAOGЁеЁїPRAЃЈAASЃЉЃЌ
ЁрOAЃНPRЃН5ЃЌ
ЙЪЕуPЕФзнзјБъЮЊЃКЉ5ЃЌ
дђyЃН![]() x2+
x2+![]() xЉ6ЃНЉ5ЃЌНтЕУЃКxЃН
xЉ6ЃНЉ5ЃЌНтЕУЃКxЃН![]() ЃЈВЛКЯЬтвтЕФжЕвбЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЕФжЕвбЩсШЅЃЉЃЌ
ЙЪЕуPЃЈ![]() ЃЌЉ5ЃЉЃЛ
ЃЌЉ5ЃЉЃЛ

ЂкЕБЕуHдкyжсЩЯЪБЃЌЭМ2гвВрЭМЃЌЭЌРэПЩЕУЃКЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЃЌЕуPЕФзјБъЮЊЃКЃЈ![]() ЃЌЉ5ЃЉЛђЃЈ
ЃЌЉ5ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ


 ПьРжаЁВЉЪПЙЎЙЬгыЬсИпЯЕСаД№АИ
ПьРжаЁВЉЪПЙЎЙЬгыЬсИпЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСйНќЖЫЮчНкЃЌФГЪГЦЗЕъУПЬьТєГі300жЛєезгЃЌТєГівЛжЛєезгЕФРћШѓЮЊ1дЊ.ОЕїВщЗЂЯжЃЌСуЪлЕЅМлУПНЕ0.1дЊЃЌУПЬьПЩЖрТєГі100жЛєезг.ЮЊСЫЪЙУПЬьЛёЕУЕФРћШѓИќЖрЃЌИУЕъОіЖЈАбСуЪлЕЅМлЯТНЕmЃЈ0<m<1ЃЉдЊЃЌ
ЃЈ1ЃЉСуЪлЕЅМлНЕМлКѓЃЌУПжЛРћШѓЮЊ дЊЃЌИУЕъУПЬьПЩЪлГі жЛєезг.
ЃЈ2ЃЉдкВЛПМТЧЦфЫћвђЫиЕФЬѕМўЯТЃЌЕБСуЪлЕЅМлЯТНЕЖрЩйдЊЪБЃЌВХФмЪЙИУЕъУПЬьЛёШЁЕФРћШѓЪЧ420дЊЃЌЧвТєГіЕФєезгИќЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
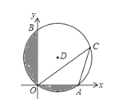
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁбDОЙ§дЕуOЃЌгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌBЕузјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌOCгыЁбDНЛгкЕуCЃЌЁЯOCAЃН30Ёу.Чѓ
ЃЉЃЌOCгыЁбDНЛгкЕуCЃЌЁЯOCAЃН30Ёу.Чѓ
ЃЈ1ЃЉЁбDЕФАыОЖЃЛ
ЃЈ2ЃЉдВжавѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєИљКХКЭІаЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯABCЕФЦНЗжЯпНЛACгкЕуEЃЌЙ§ЕуEзїBEЕФДЙЯпНЛABгкЕуFЃЌЁбOЪЧЁїBEFЕФЭтНгдВЃЎ
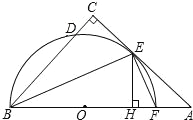
ЃЈ1ЃЉЧѓжЄЃКACЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉЙ§ЕуEзїEHЁЭABгкЕуHЃЌЧѓжЄЃКCD=HFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїBADЪЧгЩЁїBECдкЦНУцФкШЦЕуBа§зЊ60ЁуЖјЕУЃЌЧвABЁЭBCЃЌBEЃНCEЃЌСЌНгDE.
ЃЈ1ЃЉЧѓжЄЃКЁїBDEЁеЁїBCEЃЛ
ЃЈ2ЃЉЪдХаЖЯЫФБпаЮABEDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХОМУЕФПьЫйЗЂеЙЃЌЛЗОГЮЪЬтдНРДдНЪмЕНШЫУЧЕФЙизЂЃЌФГаЃбЇЩњЛсЮЊСЫНтНкФмМѕХХЁЂРЌЛјЗжРржЊЪЖ
ЕФЦеМАЧщПіЃЌЫцЛњЕїВщСЫВПЗжбЇЩњЃЌЕїВщНсЙћЗжЮЊЁАЗЧГЃСЫНтЁБЁАСЫНтЁБЁАСЫНтНЯЩйЁБЁАВЛСЫНтЁБЫФРрЃЌ
ВЂНЋМьВщНсЙћЛцжЦГЩЯТУцСНИіЭГМЦЭМЃЎ
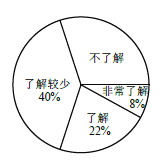

ЃЈ1ЃЉБОДЮЕїВщЕФбЇЩњЙВга__________ШЫЃЌЙРМЦИУаЃ1200 УћбЇЩњжаЁАВЛСЫНтЁБЕФШЫЪ§ЪЧ__________ШЫЃЎ
ЃЈ2ЃЉЁАЗЧГЃСЫНтЁБЕФ4 ШЫга![]() СНУћФаЩњЃЌ
СНУћФаЩњЃЌ![]() СНУћХЎЩњЃЌШєДгжаЫцЛњГщШЁСНШЫЯђШЋаЃзіЛЗБЃНЛСїЃЌЧыРћгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЧЁКУГщЕНвЛФавЛХЎЕФИХТЪЃЎ
СНУћХЎЩњЃЌШєДгжаЫцЛњГщШЁСНШЫЯђШЋаЃзіЛЗБЃНЛСїЃЌЧыРћгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЧЁКУГщЕНвЛФавЛХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCЕФИпADЫФЕШЗжЃЌЙ§УПвЛИіЗжЕузїЕзБпЕФЦНааЯпЃЌАбШ§НЧаЮЕФУцЛ§ЗжГЩЫФВПЗжS1ЁЂS2ЁЂS3ЁЂS4ЃЌдђS1ЃКS2ЃКS3ЃКS4ЕШгкЃЈЁЁЁЁЃЉ
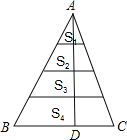
A.1ЃК2ЃК3ЃК4B.2ЃК3ЃК4ЃК5C.1ЃК3ЃК5ЃК7D.3ЃК5ЃК7ЃК9
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
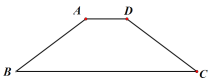
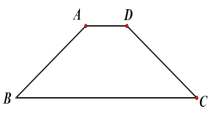
ЁОЬтФПЁПШчЭМЃЌдкЕШбќЬнаЮABCDжаЃЌAD//BC,AD=2ЃЌAB=5ЃЌBC=10ЃЌЕуEЪЧБпBCЩЯЕФвЛИіЖЏЕуЃЈВЛгыB,CжиКЯЃЉЃЌзїЁЯAEF=ЁЯAEB,ЪЙБпEFНЛБпCDгкЕуF,(ВЛгыCЃЌDжиКЯЃЉЃЌЯпЖЮBE=______________ЪБЃЌЁїABEгыЁїCEFЯрЫЦЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
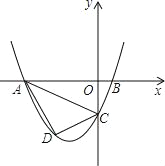
ЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+3ax+cЃЈaЃО0ЃЉгыyжсНЛгкЕуCЃЌгыxжсНЛгкAЃЌBСНЕуЃЌЕуAдкЕуBзѓВрЃЎЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌOC=3OBЃЎ
(1)жБНгаДГіCЕуЕФзјБъЃЛ
(2)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(3)ШєЕуDЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЧѓЫФБпаЮABCDУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com