
【题目】定义:若点P(a,b)在函数y= ![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=的一个“派生函数”.例如:点(2,
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y= ![]() 的图象上,则函数y=2x2+x称为函数y=
的图象上,则函数y=2x2+x称为函数y= ![]() 的一个“派生函数”.现给出以下两个命题:(1)存在函数y=
的一个“派生函数”.现给出以下两个命题:(1)存在函数y= ![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y=
的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y= ![]() 的所有“派生函数”的图象都经过同一点.下列判断正确的是( )
的所有“派生函数”的图象都经过同一点.下列判断正确的是( )
A.命题(1)与命题(2)都是真命题
B.命题(1)与命题(2)都是假命题
C.命题(1)是假命题,命题(2)是真命题
D.命题(1)是真命题,命题(2)是假命题
【答案】C
【解析】解:(1) ∵P(a,b)在y=![]() 上,
上,
∴a和b同号,
∴对称轴在y轴左侧,
∴存在函数y=![]() 的一个“派生函数”,其图像的对称轴在y轴的右侧是假命题。
的一个“派生函数”,其图像的对称轴在y轴的右侧是假命题。
(2) ∵函数y=![]() 的所有“派生函数”为y=a
的所有“派生函数”为y=a![]() +bx,
+bx,
∴x=0时,y=0,
∴所有的“派生函数”为y=a![]() +bx经过原点,
+bx经过原点,
∴y=![]() 的所有“”派生函数的图像都经过同一点是真命题。
的所有“”派生函数的图像都经过同一点是真命题。
故选C。
【考点精析】本题主要考查了二次函数的性质和命题与定理的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点P,顶点为C(1,﹣2).
(1)求此函数的关系式;
(2)作点C关于x轴的对称点D,顺次连接A,C,B,D.若在抛物线上存在点E,使直线PE将四边形ACBD分成面积相等的两个四边形,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标及△PEF的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,巳知该山坡的坡度i(即tan∠ABC)为1: ![]() ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α( 0°<α<180°),则∠α= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F. 
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y= ![]() x﹣3与反比例函数
x﹣3与反比例函数 ![]() 的图象相交于点A(4,n),与
的图象相交于点A(4,n),与 ![]() 轴相交于点B.
轴相交于点B.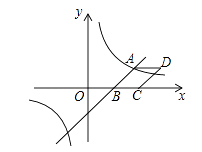
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在 ![]() 轴正半轴上,点D在第一象限,求点D的坐标;
轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 ![]() 的图象,当
的图象,当 ![]() 时,请直接写出自变量
时,请直接写出自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公交总站(A点)与B、C两个站点的位置如图所示,已知AC=6km,∠B=30°,∠C=15°,求B站点离公交总站的距离即AB的长(结果保留根号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2 , b1≠b2 , 那么称这两个一次函数为“平行一次函数”. 如图,已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com