
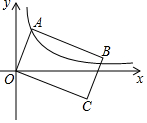
 如图,已知点A是反比例函数y=$\frac{{\sqrt{6}}}{x}$在第一象限图象上的一个动点,连接OA,以$\sqrt{3}$OA为长,OA为宽作矩形AOCB,且点C在第四象限,随着点A的运动,点C也随之运动,但点C始终在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,已知点A是反比例函数y=$\frac{{\sqrt{6}}}{x}$在第一象限图象上的一个动点,连接OA,以$\sqrt{3}$OA为长,OA为宽作矩形AOCB,且点C在第四象限,随着点A的运动,点C也随之运动,但点C始终在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -3$\sqrt{6}$ | B. | 3$\sqrt{6}$ | C. | -$\sqrt{6}$ | D. | 3$\sqrt{2}$ |
分析 设A(a,b),则ab=$\sqrt{6}$,分别过A,C作AE⊥x轴于E,CF⊥x轴于F,根据相似三角形的判定证得△AOE∽△COF,由相似三角形的性质得到OF=$\sqrt{3}$b,CF=$\sqrt{3}$b,则k=-OF•CF=-3$\sqrt{6}$.
解答 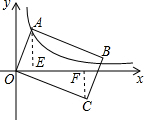 解:设A(a,b),
解:设A(a,b),
∴OE=a,AE=b,
∵在反比例函数y=$\frac{{\sqrt{6}}}{x}$图象上,
∴ab=$\sqrt{6}$,
分别过A,C作AE⊥x轴于E,CF⊥x轴于F,
∵矩形AOCB,
∴∠AOE+∠COF=90°,
∴∠OAE=∠COF=90°-∠AOE,
∴△AOE∽△COF,
∵OC=$\sqrt{3}$OA,
∴$\frac{OC}{OA}$=$\frac{OF}{AE}$=$\frac{CF}{OE}$=$\sqrt{3}$,
∴OF=$\sqrt{3}$AE=$\sqrt{3}$b,CF=$\sqrt{3}$OE=$\sqrt{3}$b,
∵C在反比例函数y=$\frac{k}{x}$的图象上,且点C在第四象限,
∴k=-OF•CF=-$\sqrt{3}$a•$\sqrt{3}$b=-3ab=-3$\sqrt{6}$,
故选A.
点评 本题主要考查了矩形的性质,相似三角形的判定和性质,反比例函数的几何意义和求法,正确作出辅助线证得△AOE∽△COF是解题的关键,同时注意k的符号.


科目:初中数学 来源: 题型:解答题
 如图,△ABC中,点A(4,0),点B在x轴上,点C在第四象限且横坐标为2,直线l1:y=-3x+3经过点B,C;直线l2经过点C,与x轴交于点P(点P在点B右侧),设点P的横坐标为m.
如图,△ABC中,点A(4,0),点B在x轴上,点C在第四象限且横坐标为2,直线l1:y=-3x+3经过点B,C;直线l2经过点C,与x轴交于点P(点P在点B右侧),设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 确定事件 | B. | 必然事件 | C. | 不可能事件 | D. | 随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.
某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.| 组别 | 获取新闻的最主要途径 | 人数 |
| A | 电脑上网 | 280 |
| B | 手机上网 | m |
| C | 电视 | 140 |
| D | 报纸 | n |
| E | 其它 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com