
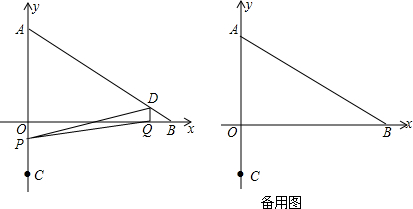
分析 (1)根据当∠PDQ=90°时,四边形POQD为矩形,再由矩形的性质解答即可;
(2)从0<t≤3、3<t≤9和9<t≤12三个时间段进行分析,求出重叠部分三角形的高,根据三角形面积公式计算即可.
解答  解:(1)∵QD⊥x轴,
解:(1)∵QD⊥x轴,
∴DQ∥AO,
∴$\frac{DQ}{AO}$=$\frac{BQ}{BO}$,即$\frac{DQ}{12}$=$\frac{2t}{24}$,
解得DQ=t,
当∠PDQ=90°时,四边形POQD为矩形,
则DQ=OP,即t=2t-6,
解得t=6;
(2)当0<t≤3时,
∵DQ∥OP,
∴$\frac{DQ}{OP}$=$\frac{QE}{EO}$,即$\frac{t}{6-2t}$=$\frac{QE}{24-2t-QE}$,
解得,QE=$\frac{24t-2{t}^{2}}{6-t}$,
则S=$\frac{1}{2}$×$\frac{24t-2{t}^{2}}{6-t}$×t=$\frac{12{t}^{2}-{t}^{3}}{6-t}$;
当3<t≤9时,
S=$\frac{1}{2}$×(24-2t)×t=12t-t2;
当9<t≤12时,
∵DQ∥OP,
∴$\frac{DQ}{PA}$=$\frac{DF}{FA}$=$\frac{QG}{GO}$,
∴$\frac{t}{2t-18}$=$\frac{QG}{24-2t-QG}$,
解得QE=$\frac{24t-{t}^{2}}{3t-18}$,
则S=$\frac{1}{2}$×$\frac{24t-{t}^{2}}{3t-18}$×t=$\frac{12{t}^{2}-{t}^{3}}{3t-18}$.
点评 本题考查的是一次函数知识的综合运用、相似三角形的性质,掌握相似扇形的对应边成比例、用运动的观点思考问题是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
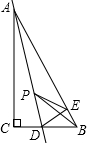 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ACD沿直线AD折叠,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ACD沿直线AD折叠,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.7×106亿元 | B. | 0.47×106亿元 | C. | 4.7×104亿元 | D. | 47×104亿元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com