
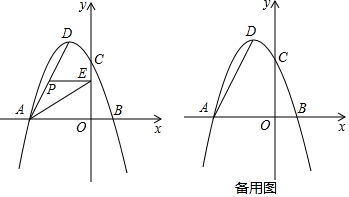
���� ��1������A�͵�B��������������ߵĽ���ʽ�õ�����a��b�ķ����飬Ȼ�����a��b��ֵ�ɵõ������ߵĽ���ʽ��Ȼ�������䷽������������ߵĽ���ʽ��
��2�������ֱ��AD�Ľ���ʽ��Ȼ��ɵõ�P��x��2x+6��������������S=$\frac{1}{2}$PE•yP�ɵõ�S��x�ĺ�����ϵʽ��Ȼ�����ö��κ��������ʿ����S�����ֵ�Լ���ʱx��ֵ��
��3����P��F��y�ύ���N������P����P��M��y�����M���ɣ�2����֪x=-$\frac{3}{2}$���ʴ˿���õ�P�͵�E�����꣬Ȼ�����÷��۵����ʵõ���PFE=��P��FE��PF=P��F=3��PE=P��E=$\frac{3}{2}$�������������÷��۵����ʺ�ƽ���ߵ����ʿ�֤����PFE=��FEN���Ӷ��ɵõ�EN=FN��Ȼ����EN=m����FN=m��P��N=3-m�����ݹ��ɶ��������m��ֵ��Ȼ�����õ�P������꣬���P���������������߽����жϼ��ɣ�
��� �⣺��1������A�͵�B���������ã�$\left\{\begin{array}{l}{9a-3b+3=0}\\{a+b+3=0}\end{array}\right.$��
��ã�a=1��b=-2��
�������ߵĽ���ʽΪy=-x2-2x+3��
��y=-x2-2x+3=-��x+1��2+4��
�������ߵĶ�������ΪDΪ��-1��4����
��2����AD�Ľ���ʽΪy=kx+b������A�͵�D���������ã�$\left\{\begin{array}{l}{-3k+b=0}\\{-k+b=4}\end{array}\right.$��
��ã�k=2��b=6��
��P��AD�ϣ�
��P��x��2x+6����
��S=$\frac{1}{2}$PE•yP=$\frac{1}{2}$��-x��•��2x+6��=-x2-3x��-3��x��-1����
�൱x=-$\frac{-3}{2����-1��}$=-$\frac{3}{2}$ʱ��Sȡֵ���ֵ$\frac{9}{4}$��
��3����ͼ1��ʾ����P��F��y�ύ���N������P����P��M��y�����M��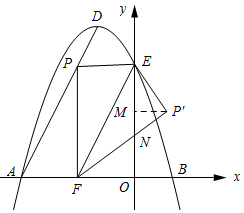
�ߵ�x=-$\frac{3}{2}$ʱ��Sȡֵ���ֵ��
��P��-$\frac{3}{2}$��3����
�ɷ��۵����ʿ�֪����PFE=��P��FE��PF=P��F=3��PE=P��E=$\frac{3}{2}$��
��PF��y�ᣮ
���PFE=��FEN��
��EN=FN��
��EN=m����FN=m��P��N=3-m��
����Rt��P��EN��P��N2+P��E2=EN2��
�ࣨ3-m��2+��$\frac{3}{2}$��2=m2����ã�m=$\frac{15}{8}$��
��S��P��EN=$\frac{1}{2}$P��N•P��E=$\frac{1}{2}$EN•P��M��
��P��M=$\frac{9}{10}$��
����Rt��EMP����EM=$\sqrt{��\frac{3}{2}��^{2}-��\frac{9}{10}��^{2}}$=$\frac{6}{5}$��
��OM=EO-EM=$\frac{9}{5}$��
��P�䣨$\frac{9}{10}$��$\frac{9}{5}$����
��x=$\frac{9}{10}$���������ߵĽ���ʽ�ã�y=$\frac{39}{100}$��$\frac{9}{5}$��
���P�䲻�ڸ��������ϣ�
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ�����κ��������ʡ����ɶ��������۵����ʣ���õ�P��������ǽ����Ĺؼ���


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{k=0}\\{b=-1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{k=2}\\{b=-3}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Ϊ����У�����˽�ѧ���·��ijߴ� | |
| B�� | �Ժ���ɻ��ϵ��㲿�����м�� | |
| C�� | ����һ���ڵ���ɱ�˰뾶 | |
| D�� | ������ʦ���ijѧ��һƪ�����еĴ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
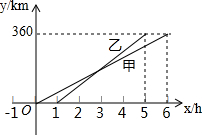 �ס����������ò�ͬ�Ľ�ͨ���ߣ���ͬһ·�ߴ�A�س���ǰ��B�أ�������ʻ��·��y��km����׳�����ʱ��x��h��֮��ĺ���ͼ����ͼ��ʾ������ͼ��õ����½��ۣ����д�����ǣ�������
�ס����������ò�ͬ�Ľ�ͨ���ߣ���ͬһ·�ߴ�A�س���ǰ��B�أ�������ʻ��·��y��km����׳�����ʱ��x��h��֮��ĺ���ͼ����ͼ��ʾ������ͼ��õ����½��ۣ����д�����ǣ�������| A�� | ���ٶ���60km/h | B�� | �ұȼ���1Сʱ���� | ||
| C�� | �ҳ���3Сʱ�ϼ� | D�� | ����AB���е㴦�ϼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У�D��б��AB���е㣬����CD������A=32�㣬���DCB�Ĵ�СΪ58�㣮
��ͼ����Rt��ABC�У�D��б��AB���е㣬����CD������A=32�㣬���DCB�Ĵ�СΪ58�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
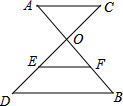 ��ͼ��AB��CD�ཻ�ڵ�O��OC=4��OD=6��AC��BD��EF�ǡ�ODB����λ�ߣ���EF=4����AC�ij�Ϊ$\frac{16}{3}$��
��ͼ��AB��CD�ཻ�ڵ�O��OC=4��OD=6��AC��BD��EF�ǡ�ODB����λ�ߣ���EF=4����AC�ij�Ϊ$\frac{16}{3}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com