
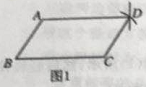
【题目】盈盈同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证
已知:如图1,在四边形ABCD中,BC=AD,________________________
求证:________________________
(1)填空,补全已知和求证
(2)按盈盈的想法写出证明
(3)用文字叙述所证命题的逆命题为________________________

【答案】 AB=CD 四边形ABCD是平行四边形 平行四边形两组对边分别相等
【解析】分析:(1)根据题意,要利用两组对边相等证明平行四边形,先找出题目命题中的已知为两组对边分别相等,即可求解,从命题“两组对边分别相等的四边形是平行四边形”中可知结论是四边形是平行四边形,根据图形和命题中的结论即可求解,
(2)连接一组对角线,可利用”边边边”定理证明两三角形全等,根据全等三角形的性质可得对应角相等,再根据内错角相等两直线平行判定两组线段平行,最后根据平行四边形的定义即可证明四边形是平行四边形.
(3)根据逆命题的条件为原命题的结论,逆命题的结论为原命题的条件即可求解.
详解:(1)AB=CD,四边形ABCD是平行四边形,
(2)证明:连接BD,
在△ABD和△CDB中,
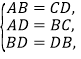 ,
,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,∠ABD=∠CDB,
∴AB∥CD,AD∥CB,
∴四边形ABCD是平行四边形,
(3)平行四边形两组对边分别相等.


科目:初中数学 来源: 题型:
【题目】先计算:
![]() =________,
=________,![]() =________,
=________,![]() =________,
=________,
![]() =________,
=________,![]() =0.
=0.
根据计算结果,回答:
(1) ![]() 一定等于a吗?如果不是,那么
一定等于a吗?如果不是,那么![]() =________;
=________;
(2)利用你总结的规律,计算:
①若x<2,则![]() =________;
=________;
②![]() =________.
=________.
(3)若a,b,c为三角形的三边长,化简:
![]() +
+![]() +
+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某运算程序,该程序是循环迭代的一种.根据该程序的指令,如果输入![]() 的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
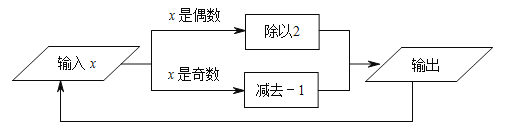
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是平面上的两定点,在平面上找一点C,使△ABC为等腰直角三角形,且点C为直角顶点,这样的点C有几个?请用尺规作图确定点C的位置,保留作图迹并说明理由
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() 图象如图,以下结论,其中正确有( )个:
图象如图,以下结论,其中正确有( )个:
①m<0;
②在每个分支上y随x的增大而增大;
③若A(﹣1,a),点B(2,b)在图象上,则a<b
④若P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.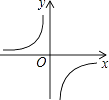
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF= . 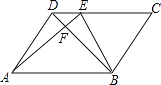
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com