
| A. | 70 | B. | 65 | C. | 60 | D. | 55 |
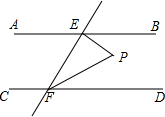
分析 先由垂直的定义,求出∠PEF=90°,然后由∠BEP=50°,进而可求∠BEF=140°,然后根据两直线平行同旁内角互补,求出∠EFD的度数,然后根据角平分线的定义可求∠EFP的度数,然后根据三角形内角和定理即可求出∠EPF的度数.
解答 解:如图所示,
∵EP⊥EF,
∴∠PEF=90°,
∵∠BEP=50°,
∴∠BEF=∠BEP+∠PEF=140°,
∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠EFD=40°,
∵FP平分∠EFD,
∴$∠EFP=\frac{1}{2}∠EFD$=20°,
∵∠PEF+∠EFP+∠EPF=180°,
∴∠EPF=70°.
故选:A.
点评 此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
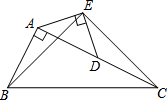 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边作等腰直角△AED,连结BE、EC.试判断线段BE和EC的数量关系和位置关系,并证明你的结论.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边作等腰直角△AED,连结BE、EC.试判断线段BE和EC的数量关系和位置关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,AB=AC,BC=6,BC边上的高AD垂直平分BC,且AD=4,以B为原点,BC所在直线为x轴,建立适当的平面直角坐标系,并求这个三角形三个顶点的坐标.
如图,已知△ABC,AB=AC,BC=6,BC边上的高AD垂直平分BC,且AD=4,以B为原点,BC所在直线为x轴,建立适当的平面直角坐标系,并求这个三角形三个顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com