
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为 . 
科目:初中数学 来源: 题型:
【题目】如图,点A,D是函数y= ![]() (k>0,x>0)图象上两点(点A在点D的左侧),直线AD分别交x,y轴于点E,F.AB⊥x轴于点B,CD⊥x轴于点C,连结AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,则S△ABD= .
(k>0,x>0)图象上两点(点A在点D的左侧),直线AD分别交x,y轴于点E,F.AB⊥x轴于点B,CD⊥x轴于点C,连结AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,则S△ABD= . 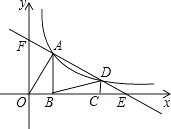
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若 ![]() =
= ![]() =
= ![]() =k(0<k<
=k(0<k< ![]() ).
).
(1)求∠PQR的度数;
(2)求证:△ARD∽△ABE;
(3)求△PQR与△ABC的面积之比(用含k的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明、小英、小丽和小华的家都在同一条街的同侧居民住宅的一排住宅楼内居住,四个家庭的住址位于同一直线上.小明家到小英家的距离约为480米,小丽家到小英家的距离约为320米,小华家在小明家和小丽家之间线段的中点的位置.
请你通过所学图形知识建立数学模型,画出图形,求出小明家和小华家的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表:
型号 | A | B |
进价 | 1800元/部 | 1500元/部 |
售价 | 2070元/部 | 1800元/部 |
(1)第一个月:用54000元购进A、B两种型号的手机,全部售完后获利9450元,求第一个月购进A、B两种型号手机的数量;
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若P,Q为某个菱形相邻的两个顶点,且该菱形的两条对角线分别与x轴,y轴平行,则称该菱形为点P,Q的“相关菱形”.图1为点P,Q的“相关菱形”的一个示意图. 
已知点A的坐标为(1,4),点B的坐标为(b,0),
(1)若b=3,则R(﹣1,0),S(5,4),T(6,4)中能够成为点A,B的“相关菱形”顶点的是;
(2)若点A,B的“相关菱形”为正方形,求b的值;
(3)⊙B的半径为 ![]() ,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围.
,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com