
����Ŀ��һ�������Ӱٻ���¥���������ͻ��������� 5 ǧ����С���ң����������� 1.5 ǧ����С��ң�Ȼ���������� 9.5 ǧ����С�ռң���ذٻ���¥��
![]()
��1���ٻ���¥Ϊԭ�㣬��Ϊ������1 ����λ���ȱ�ʾ 1 ǧ�ף������������ϱ��С����С�졢С�ռҵ�λ������С�����õ� A ��ʾ��С����õ� B ��ʾ��С�ռ��õ� C ��ʾ��
��2��С������С�ռ�����Զ��
��3��������ÿǧ���� 0.6 ������ô���������˴��ͻ������Ͷ�������
���𰸡���1����ͼ��ʾ����������2��С������С�ռ���� 8 ǧ�ף���3�����������˴��ͻ������� 11.4 ����
��������
��1��������֪���ٻ���¥Ϊԭ�㣬����Ϊ�������� 1 ����λ���ȱ�ʾ 1 ǧ��һ�������Ӱٻ���¥������������ 5 ǧ�ף�����С���ң����������� 1 .5 ǧ����С��ң�Ȼ�������� 9.5 ǧ�ף�����С�ռң���ذٻ���¥����С���ҡ�С��Һ�С�ռ��������ϵ�λ�ÿ�֪��
��2����С���ҵ������ȥ��С�ռҵ����꼴�ɣ�
��3����������һ�����ߵ�·�̣�ʵ���Ͼ��� 5+1.5+9.5+3=19��ǧ�����������ӳ����������г̹�������=������ʻÿǧ��������������ʻ���ߵ���·�̣�
��1����ͼ��ʾ��
![]()
��2��С������С�ռ���ࣺ5������3��=8��ǧ�ף���
��С������С�ռ���� 8 ǧ�ף�
��3�����������˴��ͻ������ͣ���5+1.5+9.5+3����0.6=11.4��������
�����������˴��ͻ������� 11.4 ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
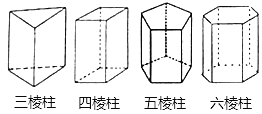
����Ŀ����ͼ�ĸ�������ֱ�������������������������������������������5���棬9���⣬6�����㣬�۲�ͼ�Σ���д����Ŀգ�
��1������������ �����棬�� �����⣬�� �������㣻
��2������������ �����棬�� �����⣬�� �������㣻
��3���ɴ˲���n�������� �����棬�� �����⣬�� �������㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�͡�ADE���й�������ĵ���ֱ�������Σ���BAC=��DAE=90�㣬��PΪ����BD��CE�Ľ��㣮
��1����֤��BD=CE��
��2����AB=2��AD=1���ѡ�ADE�Ƶ�A��ת��
�ٵ���EAC=90��ʱ����PB�ij���
��ֱ��д����ת�������߶�PB������Сֵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��C(0,-2)��ֱ��l:y=kx-2k����kȡ��ֵ��ֱ���ܹ�����B��
(1)��B������.
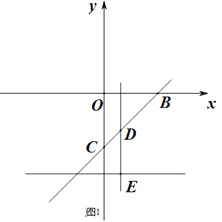
(2)��ͼ1������DΪֱ��BC�ϣ���(-1,-3)���⣩һ����,����D��x��Ĵ��߽�y= - 3�ڵ�E����F��ֱ��BC�ϣ�����D��Ϊ![]() ����λ��D�������Ϊt����DEF�����ΪS����S��t������ϵʽ.
����λ��D�������Ϊt����DEF�����ΪS����S��t������ϵʽ.
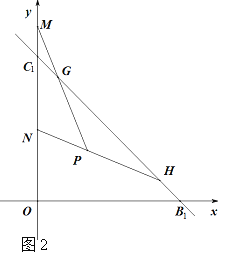
(3)��ֱ��BC����x��Գƺ�������ƽ��5����λ�õ�ֱ��B1C1����ͼ2����G(1��a)��H(6,b)��ֱ��B1C1�����㣬��P(m,n)Ϊ��һ�����ڣ�G��H������⣩��һ�㣬,��mn=6��ֱ��PG��PHΪ�ֱ�y���ڵ�MN���㣬���߶�OM��ON��ʲô������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���⻪ũ������˾����50̨�����ո�������м���20̨������30̨���Ƚ���50̨�����ո������A��B�������ո�С������30̨����A������20̨����B���������������ũ������˾�̶���ÿ������۸������
ÿ̨�����ո������� | ÿ̨�����ո������� | |
A���� | 1800 | 1600 |
B���� | 1600 | 1200 |
��1��������A����x̨���������ո��������˾��50̨�����ո��һ���õ����Ϊy��Ԫ������y��x��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2����ʹũ������˾��50̨�����ո��һ���õ�����ܶ����79 600Ԫ��˵���ж����ַ��䷽�����������ַ�����Ƴ�����
��3�����Ҫʹ��50̨�����ո��ÿ���õ������ߣ�����Ϊ�⻪ũ������˾��һ�����������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC���Ź�AB�е�D��ֱ���۵���ʹ��A����BC���ϵ�A1������Ϊ��1�β������ۺ�DE��BC�ľ����Ϊh1 �� ��ԭֽƬ���ٽ���ADE���Ź�AD�е�D1��ֱ���۵���ʹ��A����DE���ϵ�A2������Ϊ��2�β������ۺ�D1E1��BC�ľ����Ϊh2���������������ϲ�����ȥ����������2017�β�����õ����ۺ�D2016E2016 �� ��BC�ľ����Ϊh2017����h1=1����h2017��ֵΪ �� 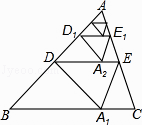
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
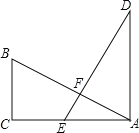
����Ŀ��(����7��)��ͼ����Rt��ABC������ACB=90�㣬EΪAC��һ�㣬��AE=BC������A��AD��CA������ΪA����AD=AC��AB��DE���ڵ�F.
��1���ж��߶�AB��DE��������ϵ��λ�ù�ϵ����˵�����ɣ�
��2������BD��BE������BC=a��AC=b��AB=c���������ı���ADBE�����֤�����ɶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AC=BC=4��D��AB���е㣬��E��F�ֱ���AC��BC�����˶�����E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�Ĺ����У���̽���� 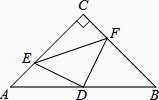
��1����֤����DFE�ǵ���ֱ�������Σ�
��2���ı���CEDF������Ƿ����仯�������仯������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com