
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在⊙
在⊙![]() 上,且
上,且![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)已知![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)EF=![]() .
.
【解析】
(1)连接OC,由AB是直径,可得∠ACB=90°,再由OA=OC,可得∠CAO=∠ACO,证明△PBC∽△PCA,可得∠PCB=∠CAO,继而可得∠OCP=90°,由此即可得结论;
(2)连接OD,先求出PA=40,然后求出OA=15,由点![]() 是
是![]() 的中点,则可得∠FOD=90°,由△PBC∽△PCA,可得
的中点,则可得∠FOD=90°,由△PBC∽△PCA,可得![]() ,证明△AEF∽△ACB,可得
,证明△AEF∽△ACB,可得![]() ,即AE=2EF,证明△DOF∽△AEF,可得
,即AE=2EF,证明△DOF∽△AEF,可得![]() ,从而求出OF=
,从而求出OF=![]() ,进而求出AF=
,进而求出AF=![]() ,在Rt△AEF中,利用勾股定理求出EF长即可.
,在Rt△AEF中,利用勾股定理求出EF长即可.
(1)连接OC,
∵AB是直径,
∴∠ACB=90°,即∠ACO+∠OCB=90°,
∵OA=OC,
∴∠CAO=∠ACO,
∵![]() ,
,
∴![]() ,
,
又∵∠P=∠P,
∴△PBC∽△PCA,
∴∠PCB=∠CAO,
∴∠PCB+∠OCB=90°,即∠OCP=90°,
∴PC是⊙O的切线;
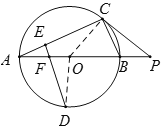
(2)连接OD,
∵![]() ,
,![]() ,
,![]() ,
,
∴PA=40,
∴AB=PA-PC=30,
∴OA=15,
∵点![]() 是
是![]() 的中点,AB是直径,
的中点,AB是直径,
∴OD=OA=15,DO⊥AB,即∠FOD=90°,
∵△PBC∽△PCA,
∴![]() ,
,
∵∠AEF=∠ACB=90°,∠A=∠A,
∴△AEF∽△ACB,
∴![]() ,即AE=2EF,
,即AE=2EF,
∵∠AEF=∠DOF=90°,∠AFE=∠DFO,
∴△DOF∽△AEF,
∴![]() ,
,
∴OF=![]() OD=
OD=![]() ,
,
∴AF=AO-OF=![]() ,
,
在Rt△AEF中,AF2=AE2+EF2,
即(![]() )2=(2EF)2+EF2,
)2=(2EF)2+EF2,
∴EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,BE,点P为DC的中点,
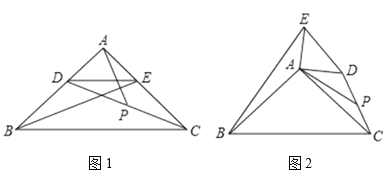
(1)(观察猜想)图1中,线段AP与BE的数量关系是 ,位置关系是 .
(2)(探究证明)把△ADE绕点A逆时针旋转到图2的位置,(1)中的猜想是否仍然成立?若成立请证明,否请说明理由;
(3)(拓展延伸)把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出线段AP长度的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
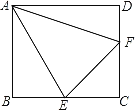
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
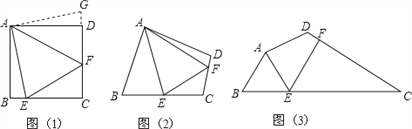
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
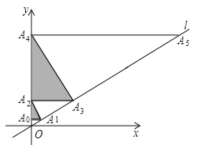
【题目】如图,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() …,这样依次下去,得到
…,这样依次下去,得到![]() ,…,其面积分别记为
,…,其面积分别记为![]() ,…,则
,…,则![]() 为__________.
为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在边BC、CD上,连接AE、EF、AF,且∠EAF=45°,下列结论:
①△ABE≌△ADF;
②∠AEB=∠AEF;
③正方形ABCD的周长=2△CEF的周长;
④S△ABE+S△ADF=S△CEF,其中正确的是_____.(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
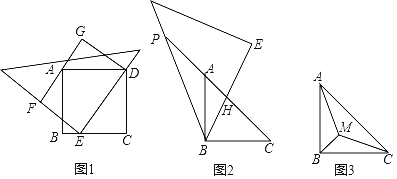
【题目】已知,把45°的直三角板的直角顶点E放在边长为6的正方形ABCD的一边BC上,直三角板的一条直角边经过点D,以DE为一边作矩形DEFG,且GF过点A,得到图1.
(1)求矩形DEFG的面积;
(2)若把正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC,把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC的直角顶点B重合,直三角板夹这个45°角的两边分别交CA和CA的延长线于点H、P,得到图2.猜想:CH、PA、HP之间的数量关系,并说明理由;
(3)若把边长为6的正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC,点M是Rt△ABC内一个动点,连接MA、MB、MC,设MA+MB+MC=y,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于点A(﹣2,﹣5),C(5,n),交y轴于点B,交x轴于点D.
的图象交于点A(﹣2,﹣5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数![]() 和一次函数y1=kx+b的表达式;
和一次函数y1=kx+b的表达式;
(2)连接OA,OC,求△AOC的面积;
(3)根据图象,直接写出y1>y2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
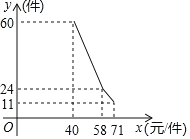
【题目】某店因为经营不善欠下38000元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息)已知该店代理的某品牌服装的进价为每件40元,该品牌服装日的售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)当销售价为多少元时,该店的日销售利润最大;
(3)该店每天支付工资和其它费用共250元,该店能否在一年内还清所有债务.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com