
【题目】观察表格:根据表格解答下列问题:
x | 0 | 1 | 2 |
ax2 | 0 | 1 | 4 |
ax2+bx+c | ﹣3 | -4 | ﹣3 |
(l)求a,b,c的值;
(2)在如图的直角坐标系中画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>﹣3成立;
(3)该图象与x轴两交点从左到右依次分别为A、B,与y轴交点为C,求过这三个点的外接圆的半径.
【答案】(1)1,﹣2,﹣3;(2)当x<0或x>2时,不等式ax2+bx+c>﹣3成立;
(3)△ABC的外接圆的半径r=O′B=![]() .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)利用描点法画出函数图象,根据图象写出函数值大于﹣3得到自变量x的取值范围即
可;
(3)想办法求出△ABC的外接圆的圆心坐标即可;
(1)由题意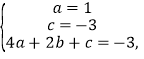 解得
解得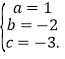
(2)函数图象如图所示:当x<0或x>2时,不等式ax2+bx+c>﹣3成立;
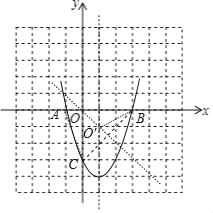
(3)由题意A(﹣1,0),B(3,0),C(0,3),
∴OB=OC=3,
∴△ABC的外接圆的圆心O′是直线y=﹣x与直线x=1的交点,
∴O′(1,﹣1),
∴△ABC的外接圆的半径![]()


科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿拉伯Al-Biruni(973年~1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》,第一题就是阿基米德的折弦定理.
阿基米德折弦定理:如图1,AB和BC是![]() 的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是
的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是![]() 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
下面是运用“截长法”证明CD=AB+BD的部分证明过程.
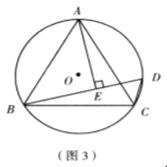
证明:如图,在CB上截取CG=AB,连接MA,MB,MC和MG.∵M是![]() 的中点, ∴MA=MC ...
的中点, ∴MA=MC ...
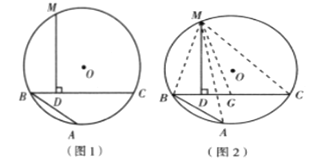
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图(3),已知等边△ABC内接于![]() ,AB=2,D为圆上一点,∠ABD=45°,AE⊥BD与点E,则△BDC的周长是 .
,AB=2,D为圆上一点,∠ABD=45°,AE⊥BD与点E,则△BDC的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
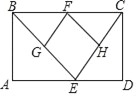
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
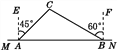
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).
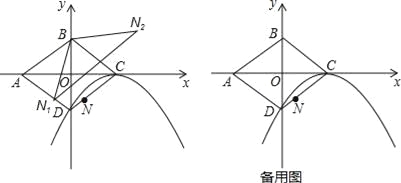
(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雄性杨树会以漫天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰.为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图.
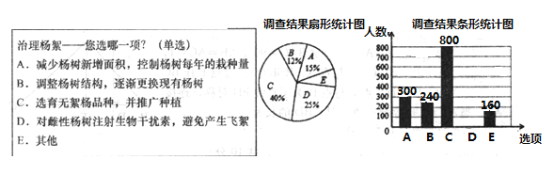
根据以上统计图,解答下列问题:
(1)本次接受调查的市民公有__________人;
(2)请补全条形统计图;
(3)扇形统计图中请求出扇形![]() 的圆心角度数.
的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() ,以
,以![]() 为公共边,在
为公共边,在![]() 两侧分别作
两侧分别作![]() 和
和![]() ,并使
,并使![]() .点
.点![]() 在射线
在射线![]() 上.
上.
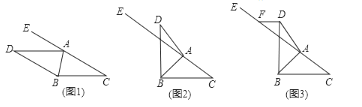
(1)如图l,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,请探究
,请探究![]() 与
与![]() 的数量关系,写出你的探究结论,并加以证明;
的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,若![]() ,过点
,过点![]() 作
作![]() 交射线于点
交射线于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有形状大小都相同的三个小球,每个小球上各标有一个数字,分别是1,2,3.现规定从布袋中任取一个小球,对应的数字作为一个两位数的十位数字;然后把小球放回袋中并搅匀,接着从袋中再任取一个小球,对应的数字作为这个两位数的个位数字.
(1)请你用画树状图或列表法分析并写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com