
 如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数. 分析 根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.
解答 解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°
∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°,
∵AP平分∠EAB
∴$∠PAB=\frac{1}{2}∠EAB$,
同理可得,$∠ABP=\frac{1}{2}∠ABC$,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA=$180°-\frac{1}{2}∠EAB-\frac{1}{2}∠ABC$=$180°-\frac{1}{2}(∠EAB+∠ABC)$=$180°-\frac{1}{2}×230°$=65°.
点评 本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.


科目:初中数学 来源: 题型:选择题
| A. | a+b | B. | 2a+b | C. | a+2b | D. | 3a+b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
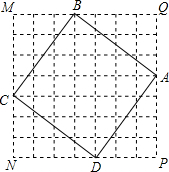 如图,在正方形网格MNPQ中,每个小方格的边长都相等,四边形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上.
如图,在正方形网格MNPQ中,每个小方格的边长都相等,四边形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察图,确定方程组$\left\{\begin{array}{l}{x-y=-1}\\{x-y=2}\end{array}\right.$的解.
观察图,确定方程组$\left\{\begin{array}{l}{x-y=-1}\\{x-y=2}\end{array}\right.$的解.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com