
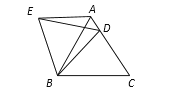
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=8,BD=6.则下列四个结论:①∠AEB=∠BDC;②AE∥BC;③△BDE是等边三角形;④△ADE的周长是14.其中正确的结论是_____(把你认为正确结论的序号都填上).
【答案】①②③④
【解析】
先根据等边三角形的性质得BA=BC,∠ABC=∠C=∠BAC=60°,再根据旋转的性质得到∠BAE=∠BCD=60°,![]() ,所以∠BAE=∠ABC=60°,则根据平行线的判定方法即可得到AE∥BC;由以上判断①②,由△BCD绕点B逆时针旋转60°,得到△BAE得到BD=BE,∠DBE=60°,则可判断△BDE是等边三角形判断③;根据等边三角形的性质得∠BDE=60°,由△BDE是等边三角形得到DE=BD=6,再利用△BCD绕点B逆时针旋转60°,得到△BAE,则AE=CD,
,所以∠BAE=∠ABC=60°,则根据平行线的判定方法即可得到AE∥BC;由以上判断①②,由△BCD绕点B逆时针旋转60°,得到△BAE得到BD=BE,∠DBE=60°,则可判断△BDE是等边三角形判断③;根据等边三角形的性质得∠BDE=60°,由△BDE是等边三角形得到DE=BD=6,再利用△BCD绕点B逆时针旋转60°,得到△BAE,则AE=CD,
所以![]() 的周长=AE+AD+DE=CD+AD+DE=AC+BD判断④.
的周长=AE+AD+DE=CD+AD+DE=AC+BD判断④.
解:∵△ABC为等边三角形, ∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,![]() ,
,
∴∠BAE=∠C=60°, ∴∠BAE=∠ABC,
∴AE∥BC,所以①②都正确;
∵△BCD绕点B逆时针旋转60°,得到△BAE,
![]() ,
,
![]() ,
,
![]()
所以△BDE是等边三角形是等边三角形,故③正确.
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∵△BDE是等边三角形, ∴DE=BD=6, 而△BCD绕点B逆时针旋转60°,得到△BAE, ∴AE=CD, 又![]() 为等边三角形,BC=8,所以AC=8,
为等边三角形,BC=8,所以AC=8,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+6=8+6=14,所以④正确.
故答案为①②③④.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为1;其中正确的结论个数有( )
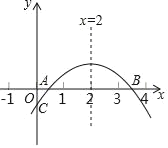
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形 AOBC 中,AC∥OB,且 OB=6,AC=5,OA=4.
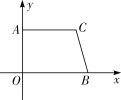
(1)求 B、C 两点的坐标;
(2)以 O、A、B、C 中的三点为顶点可组成哪几个不同的三角形?
(3)是否在边 AC 和 BC(含端点)上分别存在点 M 和点 N,使得△MON 的面积最大时,它的周长还最短?若存在,说明理由,并求出这时点 M、N 的坐标;若不存在,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
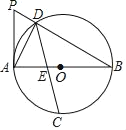
【题目】如图,AB为⊙O的直径,且AB=m(m为常数),点C为![]() 的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
(1)当DC⊥AB时,则![]() = ;
= ;
(2)①当点D在![]() 上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
②设CD长为t,求△ADB的面积S与t的函数关系式;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知四边形ABCD的是边长为4的正方形,AC为对角线,将△ACD绕点A逆时针旋转45度,得到△AEF(其中点D的对应点是点F,点C的对应点是点E),则线段CF的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
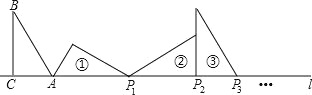
【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() ;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com