
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C.
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年度中央机关及其直属机构公务员招考网上报名已经结束,据初步统计,网上报名人数约有211.5万人,数据211.5万用科学记数法可表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC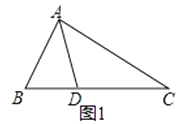
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…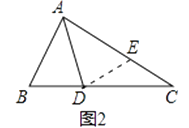
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.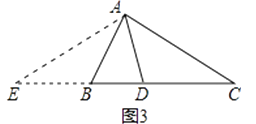
(2)【变式探究】
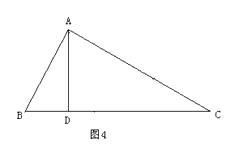
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.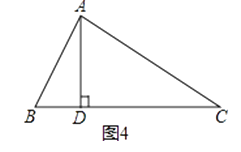
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
【问题情境】金老师给“数学小达人”小明和小军提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC.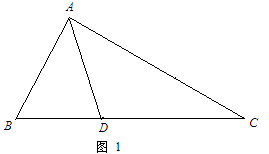
【证明思路】小明的证明思路是:如图2,在AC上截取AE=AB,连接DE.……
小军的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE.……
(1)请你从他们的思路中,任意选择一种思路继续完成下一步的证明.
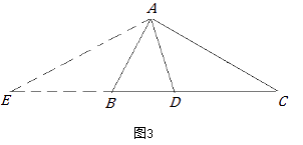
(2)【变式探究】如图4,金老师把“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变,那么AB+BD=AC还成立吗?若成立,请证明;若不成立,写出正确结论,并说明理由.
(3)【迁移拓展】如图5,△ABC中,∠B=2∠C.求证:AC2—AB2=AB×BC.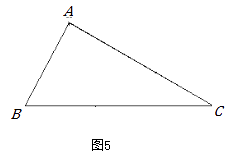
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com