
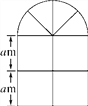
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=![]() BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=![]() BC 成立的个数有( )
BC 成立的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”。请你指出哪位同学的调查方式最合理:
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图。

请你根据以上图表提供的信息解答下列问题:
① a= , b= ;
②在扇形统计图中器乐类所对应扇形的圆心角的度数是 ;
③若我校七年级有学生480人,请你估计大约有多少学生参加武术类校本课程。
查看答案和解析>>
科目:初中数学 来源: 题型:
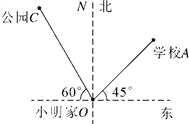
【题目】小明家O,学校A和公园C的平面示意图如图所示,图上距离OA=2cm,OC=2.5cm.
(1)学校A、公园C分别在小明家O的什么方向上?
(2)若学校A到小明家O的实际距离是400m,求公园C到小明家O的实际距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费y1与包装盒数x满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1、y2与x的函数关系式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题:
解方程![]()
解:(1)当x≥0时,
原方程化为x2 – x –2=0,
解得:x1=2,x2= - 1(不合题意,舍去)
(2)当x<0时,
原方程化为x2 + x –2=0,
解得:x1=1,(不合题意,舍去)x2= -2
∴原方程的根是x1=2, x2= - 2
(3)请参照例题解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品店购进一批单件为40元的球服,如果按单价60元销售样,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单件为多少元时,月销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足(a-![]() )2+
)2+![]() +
+![]() =0.
=0.
(1)求a,b,c的值.
(2)以a,b,c为边能否构成三角形?若能构成,求出该三角形的周长;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com