
【题目】叙述并证明三角形内角和定理.
三角形内角和定理: ;
已知:如图△ABC.
求证: .
证明:

【答案】三角形的内角和是180°;∠A+∠B+∠C=180°;证明见解析.
【解析】
要证明三角形的三个内角的和为180°,可以把三角形三个角转移到一个平角上,利用平角的性质解答.
解:定理:三角形的内角和是180°;
已知:如图△ABC;
求证:∠A+∠B+∠C=180°.
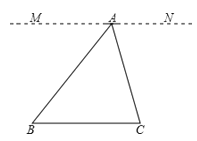
证明:过点作直线MN,使MN//BC.
∵MN∥BC,
∴∠B=∠MAB,∠C=∠NAC(两直线平行,内错角相等)
又∵∠MAB+∠NAC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)即∠A+∠B+∠C=180°.
故答案为:三角形的内角和是180°;∠A+∠B+∠C=180°;证明见解析.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
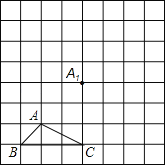
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.
(3)连结![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
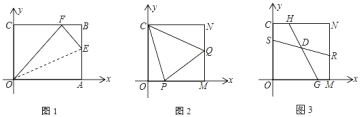
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“三角形的一个外角等于与它不相邻的两个内角的和”揭示了三角形的一个外角与它的两个内角之间的数量关系,请探索并写出三角形没有公共顶点的两个外角与它的第三个内角之间的关系:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.将这次调查情况整理并绘制如下两幅统计图如图2:

根据图中的信息,解答下列问题:
(1)本次活动共有 位市民参与调查;
(2)补全条形统计图和扇形统计图;
(3)扇形统计图中A项所对应的圆心角的度数为
(4)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和频数分布直方图:
次数 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
频数 | a | 4 | 12 | 16 | 8 | 3 |
结合图表完成下列问题:
(1)a= ,全班人数是______;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀学生人数占全班总人数的百分之几?

查看答案和解析>>
科目:初中数学 来源: 题型:
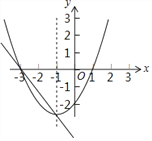
【题目】已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
①二次函数y1有最大值;
②二次函数y1的图象关于直线x=﹣1对称
③当x=﹣2时,二次函数y1的值大于0
④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<﹣3或m>﹣1.
以上推断正确的是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
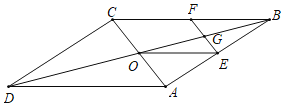
(1)证明:四边形![]() 是平行四边形
是平行四边形
(2)点![]() 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com