
【题目】某游泳馆每年夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费4元;方式二:不购买会员证,每次游泳付费10元.设小明计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 140 | 160 | _______ | … | _______ |
方式二的总费用(元) | 100 | 150 | ________ | … | ________ |
(2)若小明计划今年夏季游泳的总费用为260元,选择哪种付费方式,他游泳的次数比较多?
(3)小明选择哪种付费方式更合算?并说明理由.
【答案】(1)180;![]() ;200;
;200;![]() ;(2)小明选择方式一游泳次数比较多;(3)当
;(2)小明选择方式一游泳次数比较多;(3)当![]() 时,有
时,有![]() ,小明选择方式二更合算;当
,小明选择方式二更合算;当![]() 时,有
时,有![]() ,小明选择方式一更合算
,小明选择方式一更合算
【解析】
(1)根据两种付费分式计算、列式、填表即可;(2)根据(1)中所得关系式,代入求出x值,比较即可得答案;(3)设方式一与方式二的总费用的差为y元,求出y与x的关系式,根据一次函数的性质即可得答案.
(1)方式一:100+4×20=180(元),4x+100;
方式二:10×20=200(元),10x;
故答案为:180;![]() ;200;
;200;![]() .
.
(2)方式一:![]() ,
,
解得![]() .
.
方式二:![]() ,
,
解得![]() .
.
∵![]() ,
,
∴小明选择方式一游泳次数比较多.
(3)设方式一与方式二的总费用的差为y元.
则![]() ,即
,即![]()
当![]() 时,即
时,即![]() ,得
,得![]() .
.
∵![]() ,
,
∴y随x的增大而减小.
∴当![]() 时,有
时,有![]() ,小明选择方式二更合算;
,小明选择方式二更合算;
当![]() 时,有
时,有![]() ,小明选择方式一更合算.
,小明选择方式一更合算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,是全国最大的瓷碗造型建筑,座落于江西景德镇,整体造型概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为了计算该建筑物横断面(瓷碗橫断面ABCD为等腰梯形)的高度,如图2,她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°,而后沿着一段坡度为0.44(坡面与水平线夹角的正切值)的小坡PQ步行到点Q(此过程中AD,AP,PQ始终处于同一平面)后测得点D的仰角减少了5°.已知坡面PQ的水平距离为20米,小敏身高忽略不计,试计算该瓷碗建筑物的高度.(参考数据:sin 40°≈0.64,tan 40°≈0.84)
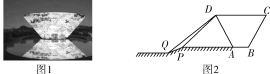
查看答案和解析>>
科目:初中数学 来源: 题型:
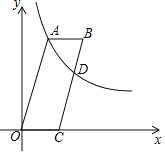
【题目】如图,在平面直角坐标系中,OABC的顶点C在x轴上,函数y=![]() (k>0,x>0)的图象经过点A(2,6),且与边BC交于点D.若点D是边BC的中点,则OC的长为( )
(k>0,x>0)的图象经过点A(2,6),且与边BC交于点D.若点D是边BC的中点,则OC的长为( )
A. 2B. 2.5C. 3.5D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个水库的水位在某段时间内持续上涨,表记录了连续5小时内6个时间点的水位高度,其中![]() 表示时间,
表示时间,![]() 表示水位高度.
表示水位高度.
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 3 | 3.3 | 3.6 | 3.9 | 4.2 | 4.5 | … |
(1)通过观察数据,请写出水位高度![]() (米)与时间
(米)与时间![]() (小时)的函数解析式(不需要写出定义域);
(小时)的函数解析式(不需要写出定义域);
(2)据估计,这种上涨规律还会持续,并且当水位高度达到8米时,水库报警系统会自动发出警报,请预测再过多久系统会发出警报.
查看答案和解析>>
科目:初中数学 来源: 题型:
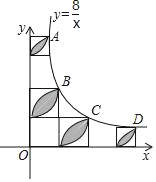
【题目】已知,A、B、C、D是反比例函数y=![]() (x>0)图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是__________(用含π的代数式表示).
(x>0)图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是__________(用含π的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,则组成第4个图案的基础图形的个数为( ).

A. 11B. 12C. 13D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击运动员练习射击,5次成绩分别是:8、9、7、8、x(单位:环).下列说法中正确的是( )
A. 若这5次成绩的中位数为8,则x=8
B. 若这5次成绩的众数是8,则x=8
C. 若这5次成绩的方差为8,则x=8
D. 若这5次成绩的平均成绩是8,则x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题
定义:如果四边形的某条对角线平分一组角,那么把这条对角线叫“美妙线”,该四边形叫做“美妙四边形”.
如图:在四边形ABCD中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”,四边形ABCD就称为“美妙四边形”.
问题:(1)下列四边形中是“美妙四边形”的有_______个.
①平行四边形 ②矩形 ③菱形 ④正方形
A.1 B. 2 C. 3 D.4
(2)四边形ABCD是“美妙四边形”,AB=3+![]() ,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.
,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.
(3)如图,若△ABC中,AB=3,BC=4,∠B=90°,将△ABC扩充成以AC为“美妙线”的“美妙四边形”ABCD,试求D到BC的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com