
【题目】陶军于上周购买某农产品10000斤,每斤![]() 元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤
元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤![]() 元)
元)
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天的价格涨跌情况(元) |
|
|
|
|
|
当天的交易量(斤) | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品价格为每斤多少元?
(2)本周内该农产品的最高价格为每斤多少元?最低价格为每斤多少元?
(3)陶军在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
【答案】(1)3.35元;(2)本周内该农产品的最高价格为每斤3.35元,最低价格为每斤2.85元;(3)陶军在本周的买卖中共赚了6325元.
【解析】
(1)根据购进当日该农产品的批发价格为每斤![]() 元,再结合周一到周四的涨跌情况即可得出结果;
元,再结合周一到周四的涨跌情况即可得出结果;
(2)根据每日的涨跌情况,计算出每日的价格即可得出结果;
(3)根据陶军在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,利用售价-进价-摊位费用=收益即可求解.
解:(1)2.7+0.3-0.1+0.25+0.2=3.35(元);
(2)星期一的价格为:2.7+0.3=3(元);
星期二的价格为:3-0.1=2.9(元);
星期三的价格为:2.9+0.25=3.15(元);
星期四的价格为:3.15+0.2=3.35(元);
星期五的价格为:3.35-0.5=2.85(元).
所以本周内该农产品的最高价格为每斤3.35元,最低价格为每斤2.85元.
(3)(2500×3-5×20)+(2000×2.9-4×20)+(3000×3.15-3×20)+(1500×3.35-2×20)+(1000×2.85-20)-10000×2.4
=7400+5720+9390+4985+2830-24000
=6325(元)
答:陶军在本周的买卖中共赚了6325元.


科目:初中数学 来源: 题型:
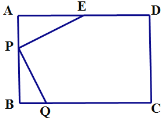
【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并直接写出此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙出发沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示,下列说法:
的函数函数图像的一部分如图所示,下列说法:
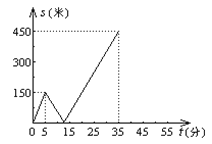
①甲行走的速度是30米/分;
②乙出发12.5分钟后追上甲;
③甲比乙晚到图书馆20分钟;
④甲行走30.5分钟或38分钟时,甲、乙两人相距360米;
其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.
(1)当m取何值时,此方程有两个不相等的实数根;
(2)当抛物线y=mx2+(3m+1)x+3与x轴两个交点的横坐标均为整数,且m为正整数时,求此抛物线的解析式;
(3)在(2)的条件下,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象直接写出实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
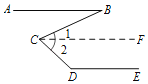
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°.
证明:过点C作CF∥AB.
∵CF∥AB(已作),
∴∠1= .
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B .
∵AB∥DE,CF∥AB(已知),
∴CF∥DE
∴∠D+∠2=180°
∴∠D+∠BCD﹣∠B=180° .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:将任意三个互不相等的数a,b,c按照从小到大的顺序排列后,把处于中间位置的数叫做这三个数的中位数.用符号mid{a,b,c}表示.例如mid{﹣1,2,1}=1.
(1)mid{![]() ,5,3}= .
,5,3}= .
(2)当x<﹣2时,求mid{1+x,1﹣x,﹣1}.
(3)若x≠0,且mid{5,5﹣2x,2x+1}=2x+1,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:
在一个三角形中,如果一个角的度数是另一个角的度数![]() 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为
倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为![]() ,
,![]() ,
,![]() 的三角形是“和谐三角形”
的三角形是“和谐三角形”
概念理解:
如图,![]() ,在射线
,在射线![]() 上找一点
上找一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为端点作射线
为端点作射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与
不与![]() 重合)
重合)
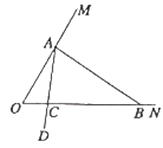
(1)![]() 的度数为 ,
的度数为 ,![]() (填“是”或“不是”)“和谐三角形”
(填“是”或“不是”)“和谐三角形”
(2)若![]() ,求证:
,求证:![]() 是“和谐三角形”.
是“和谐三角形”.
应用拓展:
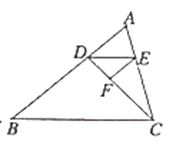
如图,点![]() 在
在![]() 的边
的边![]() 上,连接
上,连接![]() ,作
,作![]() 的平分线
的平分线![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,
,![]() .若
.若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动______ 秒时,△DEB与△BCA全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com