
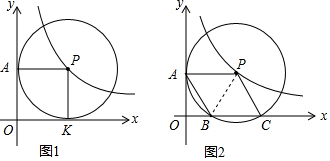
分析 (1)先利用切线的性质得出四边形OAPK是矩形,再判断出PA=PK即可得出结论;
(2)先求出BC=2,再用菱形的性质得出AP=PC=BC=2,另为用圆的性质得出PB=PC,用勾股定理求出PD即可得出点P坐标,最后代入即可.
解答 解:(1)四边形OAPK是正方形,
理由:∵P为圆心的圆始终与y轴相切,设切点为A.
∴∠OAP=90°,
∵⊙P运动到与x轴也相切于K点,
∴∠OKP=90°,
∵∠AOK=90°,
∴∠OAP=∠AOK=∠OKP=90°,
∴四边形OAPK是矩形,
∵⊙P和x,y轴都相切,
∴AP=KP,
∴矩形OAPK是正方形.
(2)如图,
∵B(1,0)、C(3,0),
∴BC=2,
∵四边形ABCP为菱形,
∴AP=PC=BC=2,
连接BP,
∴BP=PC=BC=2,
∴△PBC是等边三角形,
过点P作PD⊥BC,
∴BD=CD=$\frac{1}{2}$BC=1,
在Rt△BPD中,BP=2,PD=$\sqrt{3}$,
∴P(2,$\sqrt{3}$),
∵点P是反比例函数y=$\frac{k}{x}$图象上,
∴k=2×$\sqrt{3}$=2$\sqrt{3}$,
∴反比例函数的解析式为y=$\frac{2\sqrt{3}}{x}$.
点评 此题是反比例函数综合题,主要考查了切线的性质,菱形,矩形,正方形的判定,勾股定理,等边三角形的性质.待定系数法,掌握特殊四边形的性质和判定以及等边三角形的性质是解本题的关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:
如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
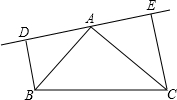 如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;若B,C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC.
如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;若B,C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
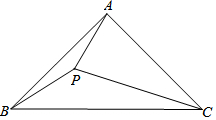 已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.
已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
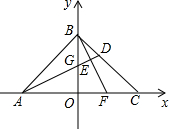 如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.
如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
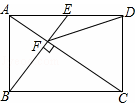 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
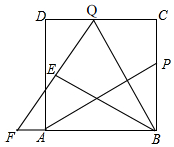 如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com