练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，弦OC，FE的延长线交于圆外一点P，割线PAB经过圆心O，请你结合现有图形，添加一个适当的条件:________，使∠1=∠2．

    答案：略
    解析：

    或CD=EF


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

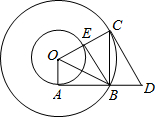    如图所示，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于点B，大圆的精英家教网弦BC⊥AB于点B，过点C作大圆的切线CD交AB的延长线于点D，连接OC交小圆于点E，连接BE、BO．
    （1）求证：△AOB∽△BDC；
    （2）设大圆的半径为x，CD的长为y：
    ①求y与x之间的函数关系式；
    ②当BE与小圆相切时，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：022

    如图所示，弦OC，FE的延长线交于圆外一点P，割线PAB经过圆心O，请你结合现有图形，添加一个适当的条件:________，使∠1=∠2．

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年浙江杭州萧山回澜初中九年级12月阶段性测试数学试卷（解析版） 题型：解答题

    小明和同桌小聪在课后做作业时，对课本中的一道作业题，进行了认真探索．

    【作业题】如图1，一个半径为100m的圆形人工湖如图所示，弦AB是湖上的一座桥，测得圆周角∠C=45°，求桥AB的长．

    小明和小聪经过交流，得到了如下的两种解决方法：

    方法一：延长BO交⊙O与点E，连接AE，得 Rt△ABE，∠E=∠C，∴AB=；

    方法二：作AB的弦心距OH，连接OB， ∴∠BOH=∠C，解Rt△OHB， ∴HB=，∴AB=．

    感悟：圆内接三角形的一边和这边的对锐角、圆的半径（或直径）这三者关系，可构成直角三角形，从而把一边和这边的对锐角﹑半径建立一个关系式．

    （1）问题解决：受到（1）的启发，请你解下面命题：如图2，点A（3，0）、B（0，），C为直线AB上一点，过A、O、C的⊙E的半径为2．求线段OC的长．

    （2）问题拓展：如图3，△ABC中，∠ ACB=75°，∠ABC=45°，AB=，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连结EF， 设⊙O半径为x， EF为y．①y关于x的函数关系式；②求线段EF长度的最小值．

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小明和同桌小聪在课后做作业时，对课本中的一道作业题，进行了认真探索。

    【作业题】如图1，一个半径为100m的圆形人工湖如图所示，弦AB是湖上的一座桥，测得圆周角∠C=45°,求桥AB的长。

    小明和小聪经过交流，得到了如下的两种解决方法：

    方法一：延长BO交⊙O与点E，连接AE，得 Rt△ABE，∠E=∠C，∴AB=100；

    方法二：作AB的弦心距OH，连接OB, ∴∠BOH=∠C，解Rt△OHB, ∴HB=50，

    ∴AB=100。

    感悟：圆内接三角形的一边和这边的对锐角、圆的半径(或直径)这三者关系，

    可构成直角三角形，从而把一边和这边的对锐角﹑半径建立一个关系式。

    （1）问题解决：受到(1)的启发，请你解下面命题：如图2，点A（3，0）、B（0，），C为直线AB上一点，过A、O、C的⊙E的半径为2. 求线段OC的长。

    （2）问题拓展：如图3，△ABC中，∠ ACB=75°，∠ABC=45°，AB=2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连结EF, 设⊙O半径为x, EF为y.

    ①     y关于x的函数关系式；②求线段EF长度的最小值。

    查看答案和解析>>

    同步练习册答案