
【题目】如图,在□ABCD中,AB=10,BC=5,BN平分∠ABC交CD于点N,交AD的延长线于点M,则下列结论:①DM=5;②线段BM、CD互相平分;③BD⊥AM;④△BCN是等边三角形;⑤AN⊥BM,其中正确的有______________(填序号).

【答案】①②⑤
【解析】
①通过判断![]() ,即可得到
,即可得到![]() ;②通过判断
;②通过判断![]() ,即可得到
,即可得到![]() ,
,![]() ,即可得到线段BM、CD互相平分;③由于无法求证BA=BM从而无法得到BD⊥AM;④根据题意求证
,即可得到线段BM、CD互相平分;③由于无法求证BA=BM从而无法得到BD⊥AM;④根据题意求证![]() 是等腰三角形但不是等边三角形;⑤通过求证
是等腰三角形但不是等边三角形;⑤通过求证![]() 是等腰三角形,再根据三线合一即可得解.
是等腰三角形,再根据三线合一即可得解.
①∵四边形ABCD是平行四边形
∴![]() ,
,![]()
∴![]() ,
,![]()
∵BN平分∠ABC
∴![]()
∴![]()
∴![]()
∵BC=5,AB=10
∴![]()
在![]() 与
与![]() 中
中
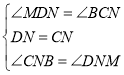
∴![]()
∴![]() ,故①正确;
,故①正确;
②∵![]()
∴![]()
又∵![]()
∴线段BM、CD互相平分,故②正确;
③∵由四边形ABCD是平行四边形得![]()
∴![]()
但是题中条件不足以证明![]() ,则无法根据三线合一求证BD⊥AM,故③错误;
,则无法根据三线合一求证BD⊥AM,故③错误;
④由①可知![]() ,但是无法证明
,但是无法证明![]() ,故④错误;
,故④错误;
⑤由③得![]() ,由②得
,由②得![]() ,则由三线合一可知AN⊥BM,故⑤正确,
,则由三线合一可知AN⊥BM,故⑤正确,
综上,正确的有①②⑤,
故答案为:①②⑤.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF. 
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形向右平移3个单位长度,再向上平移2个单位长度,则平移后三个顶点的坐标为( )
A.(-1,-1),(2,3),(5,1)
B.(-1,1),(3,2),(5,1)
C.(-1,1),(2,3),(5,1)
D.(1,-1),(2,2),(5,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
A.46°
B.47°
C.48°
D.49°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°。将求∠AGD的过程填写完整,并将依据填到相应的括号内.

解:∵EF∥AD( )
∴∠2= 。( )
又∵∠1=∠2,( )
∴∠1=∠3。( )
∴AB∥ 。( )
∴∠BAC+ =180。( )
又∵∠BAC=70°,
∴∠AGD= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在 ![]() 中,
中, ![]() ,
, ![]() .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为 ![]() ,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米∕秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:

(1)平移到1.5秒时,重叠部分的面积为 厘米2.
(2)求小正方形在平移过程中,S与t的关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学三次到某超市购买A、B两种商品,其中仅有一次是由折扣的,购买数量及消费金额如下表:
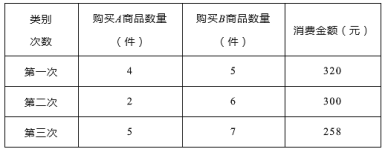
解答下列问题:
(1)第_______次购买的商品有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,则折扣数为______折;
(4)小明同学再次购买A、B两种商品共10件,在(3)的折扣数的前提下,这10件商品的消费金额不超过200元,求至少购买A商品的件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
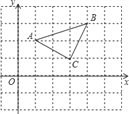
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com