
【题目】如图,已知![]() 的顶点
的顶点![]() 和
和![]() 边的中点
边的中点![]() 都在双曲线
都在双曲线![]() 的一个分支上,点
的一个分支上,点![]() 在
在![]() 轴上,
轴上,![]() 于
于![]() ,则
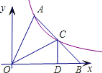
,则![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
过点A作AM⊥OB于M,设点A坐标为(x,y),根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=![]() |k|.可求出S△AMO和S△AMB,进而求出S△AOB,又因为C为AB中点,所以△AOC的面积为△AOB面积的一半,问题得解.
|k|.可求出S△AMO和S△AMB,进而求出S△AOB,又因为C为AB中点,所以△AOC的面积为△AOB面积的一半,问题得解.
过点A作AM⊥OB于M,设点A坐标为(x,y),
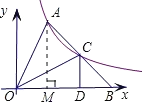
∵顶点A在双曲线y=![]() (x>0)图象上,
(x>0)图象上,
∴xy=4,
∴S△AMO=![]() OMAM=
OMAM=![]() xy=2,
xy=2,
设B的坐标为(a,0),
∵中点C在双曲线y=![]() (x>0)图象上,CD⊥OB于D,
(x>0)图象上,CD⊥OB于D,
∴点C坐标为(![]() ,
,![]() ),
),
∴S△CDO=![]() ODCD=
ODCD=![]()
![]()
![]() =2,
=2,
整理,ay+xy=16,
∵xy=4,
∴ay=164=12,
又∵C为AB中点,
∴△AOC的面积为![]() ×6=3.
×6=3.
故选:B.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,边
中,边![]() ,
,![]() ,以点
,以点![]() 为原点,
为原点,![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴和
轴和![]() 轴,建立直角坐标系.
轴,建立直角坐标系.
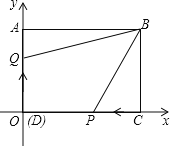
(1)点![]() 的坐标为
的坐标为![]() ,则
,则![]() 点坐标为______,
点坐标为______,![]() 点坐标为______;
点坐标为______;
(2)当点![]() 从
从![]() 出发,以2单位/秒的速度沿
出发,以2单位/秒的速度沿![]() 方向移动(不过
方向移动(不过![]() 点),
点),![]() 从原点
从原点![]() 出发以1单位/秒的速度沿
出发以1单位/秒的速度沿![]() 方向移动(不过
方向移动(不过![]() 点),
点),![]() ,
,![]() 同时出发,在移动过程中,四边形
同时出发,在移动过程中,四边形![]() 的面积是否变化?若不变,求其值;若变化,求其变化范围.
的面积是否变化?若不变,求其值;若变化,求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图![]() ,把
,把![]() 沿直线
沿直线![]() 平行移动线段
平行移动线段![]() 的长度,可以变到
的长度,可以变到![]() 的位置;
的位置;
如图![]() ,以
,以![]() 为轴,把
为轴,把![]() 翻折
翻折![]() ,可以变到
,可以变到![]() 的位置;
的位置;
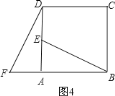
如图![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 旋转
旋转![]() ,可以变到
,可以变到![]() 的位置.
的位置.
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图![]() 中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使
中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使![]() 变到
变到![]() 的位置;
的位置;
②指图中线段![]() 与
与![]() 之间的关系,为什么?
之间的关系,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
![]() 求直线
求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标及
的坐标及![]() 的面积;
的面积;
![]() 在
在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的值最大?若存在,直接写出点
的值最大?若存在,直接写出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 当点
当点![]() 在双曲线上运动时,作以
在双曲线上运动时,作以![]() 、
、![]() 为邻边的平行四边形,求平行四边形周长最小时点
为邻边的平行四边形,求平行四边形周长最小时点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,将![]() 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
(1)若点D恰好与点O重合,则∠ABC= °;
(2)延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点为
,顶点为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过
经过![]() 、
、![]() 两点,交抛物线的对称轴于点
两点,交抛物线的对称轴于点![]() ,其中点
,其中点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求
,求![]() 的周长;
的周长;
(3)若![]() 是抛物线位于直线
是抛物线位于直线![]() 的下方且在其对称轴左侧上的一点,当四边形
的下方且在其对称轴左侧上的一点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com