
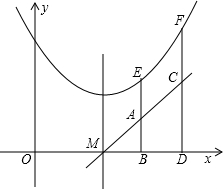
 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )| A. | S=y2+y1 | B. | S=y2+2y1 | C. | S=y2-y1 | D. | S=y2-2y1 |
分析 首先根据题意可求得:y1,y2的值,A与C的坐标,即可用x1与x2表示出AB,CD,BD的值,易得四边形ABCD是直角梯形,即可得S=$\frac{1}{2}$(AB+CD)•BD,然后代入其取值,整理变形,即可求得S与y1、y2的数量关系式.
解答 解:根据题意得:y1=ax12+bx1+c,y2=ax22+bx2+c,
点A的坐标为:(x1,2ax1+b),点C的坐标为:(x2,2ax2+b),
∴AB=2ax1+b,CD=2ax2+b,BD=x2-x1,
∵EB⊥BD,CD⊥BD,
∴AB∥CD,
∴四边形ABCD是直角梯形,
∴S=$\frac{1}{2}$(AB+CD)•BD=$\frac{1}{2}$(2ax1+b+2ax2+b)(x2-x1)=a(x2+x1)(x2-x1)+b(x2-x1)=(ax22+bx2)-(ax12+bx1)=(ax22+bx2+c)-(ax12+bx1+c)=y2-y1.
即S=y2-y1.
故选C.
点评 此题考查了二次函数与一次函数的综合应用问题.此题难度较大,解题的关键是抓住点与函数的关系,注意根据整式的运算法则将原整式变形,注意数形结合思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
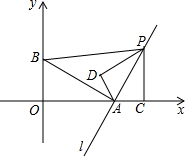 如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为P(5,2),p(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为P(5,2),p(8,8),P(0,-8),P(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
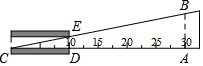 如图是测量玻璃管内径的示意图,点D正对“10mm”刻度线,点A正对“30mm”刻度线,DE∥AB.若量得AB的长为6mm,则内径DE的长为2mm.
如图是测量玻璃管内径的示意图,点D正对“10mm”刻度线,点A正对“30mm”刻度线,DE∥AB.若量得AB的长为6mm,则内径DE的长为2mm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
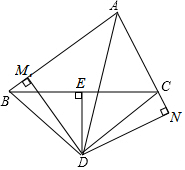 如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )
如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )| A. | DM=DN | B. | ∠ABD+∠ACD=180° | ||
| C. | AC+AN=AB | D. | BC2+4DE2=4BM2+4DM2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=2,BC=5,则EF的值是$\sqrt{10}$.
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=2,BC=5,则EF的值是$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com