
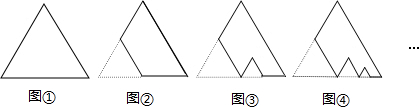
分析 根据等边三角形的性质得出,三角形的边长分别为:$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$…,即相邻三角形相似比为1:2,进而求出相邻三角形面积比,从而得出规律.
解答 解:∵依次剪去一块更小的正三角形纸板,即其边长为前一块被剪掉正三角形纸板边长的$\frac{1}{2}$,
∴三角形的边长分别为:$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$…
即相邻三角形相似比为:1:2,
∴相邻三角形面积比为:1:4,
∴剪去一块的正三角形纸板面积分别为:$\frac{\sqrt{3}}{4}$,$\frac{\sqrt{3}}{16}$,$\frac{\sqrt{3}}{64}$,$\frac{\sqrt{3}}{256}$…
第n个纸板的面积为:$\frac{\sqrt{3}}{{4}^{n}}$,
第n-1个纸板的面积为:$\frac{\sqrt{3}}{{4}^{n-1}}$,
∴Sn-1-Sn=$\frac{\sqrt{3}}{{4}^{n-1}}$$-\frac{\sqrt{3}}{{4}^{n}}$=$\frac{3\sqrt{3}}{{4}^{n}}$,
故答案为:$\frac{3\sqrt{3}}{{4}^{n}}$.
点评 此题主要考查了等边三角形的性质与数据的规律性知识,此题得出相邻三角形面积比,从而表示出各三角形面积是解决问题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右依次记为A1、A2、A3、…、An,已知第1个正方形中的一个顶点A1的坐标为(1,1),则点A2015的纵坐标为( )
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右依次记为A1、A2、A3、…、An,已知第1个正方形中的一个顶点A1的坐标为(1,1),则点A2015的纵坐标为( )| A. | 2015 | B. | 2014 | C. | 22014 | D. | 22015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,设一个三角形的三边分别是3,1-3m,8.
如图,设一个三角形的三边分别是3,1-3m,8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
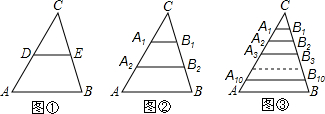
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
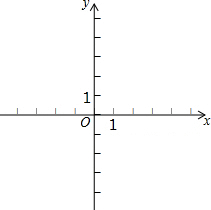 在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$(x+m)2的顶点为A,直线y=-x-m与y轴相交于点B,其中m>0.
在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$(x+m)2的顶点为A,直线y=-x-m与y轴相交于点B,其中m>0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 初中生的视力状况受到全社会的广泛关注,某市有关部门对全市24000名初中生视力状况进行了一次抽样调查,如图是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数),根据图中所提供的信息,回答下列问题:
初中生的视力状况受到全社会的广泛关注,某市有关部门对全市24000名初中生视力状况进行了一次抽样调查,如图是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数),根据图中所提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
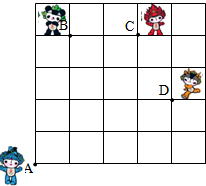 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com