
 如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:
如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:分析 (1)由函数图象可知:在气温T随时间t的变化过程中有两个变量T和t,对于每一个t(时)值都有唯一一个T(℃)值和它对应,所以气温T(℃)与时间t(时)的关系符合函数关系;
(2)因为函数图象上的每一个点的横坐标表示这一天中的某一时刻,纵坐标表示其对应的气温,所以,当t=12时,T=10,即12时的气温是8℃;
(3)函数图象上最高点对应的纵坐标表示的函数值最大,相反函数图象上最低点对应的纵坐标表示的函数值最少,观察、分析函数图象即可求解;
(4)当气温T=4℃,对应的t的值不唯一,观察图象可知,这一天当中8时、22时的气温为4℃.
解答 解:(1)因为,一般地,如果在一个变化过程中有两个变量x和y,并且对于x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,
而由该函数的图象可知,在气温T随时间t的变化过程中有两个变量T和t,并且对于t的每一个值,变量T都有唯一的值与它对应,那么我们称T是t的函数,
所以,气温T(℃)是时间t(时)的函数.
(2)因为函数图象中的横坐标表示某一天当中的某一时刻,而纵坐标表示某一时刻的气温,
所以,12时的气温是8℃.
(3)因为,函数图象上最高点对应的纵坐标表示的函数值最大,相反函数图象上最低点对应的纵坐标表示的函数值最少,
所以,通过审图可知,这一天中:
14时的气温最高,是10℃;4时的气温最低,是零下2℃
(4)过纵轴上4对应的点作纵坐标轴的垂线,与函数图象相交的点对应的横坐标即为气温为4℃时的时刻,
所以,由函数图象可知,这一天中:8时、22时的气温是4℃.
点评 主要考查了函数图象的读图能力.要能根据函数图象的性质、意义和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义回答问题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
| A. | a≥b | B. | a≤b | C. | a>b>0 | D. | a<b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF.
已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
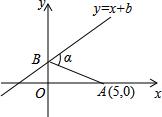 如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{1-4y}{3}$ | B. | x=$\frac{4y-1}{3}$ | C. | x=$\frac{1+4y}{3}$ | D. | y=$\frac{3x-1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com