
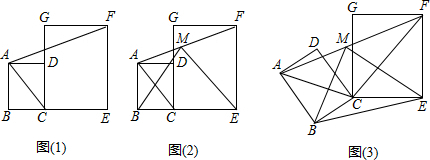
分析 (1)因为矩形ABCD与矩形CEFG的长与宽的比均为$\sqrt{3}$:1,所以,延长AD交EF与点H,由已知条件可求得FH的长,再由勾股定理求得AF的长.
(2)延长BM、EF相交于点P,先证△ABM≌△FPM可得BM=PM,再证题目中的提示可知ME=$\frac{1}{2}$BP=BM,然后设法证明∠PBE=60°.
(3)根据题目特点可利用代数法求解:设BC=1,旋转角为α,建立直角坐标系,根据题目条件求出点A、B、E、F、M的坐标,然后利用勾股定理求得线段BM、BE、EM的长判定△BME的形状.
解答 解:(1)连接CF,延长AD交EF于点H,
∵四边形ABCD是矩形,
∴∠ABC=90°.
又∵AB:BC=$\sqrt{3}$:1且BC=2,
∴AB=2$\sqrt{3}$,AC=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$═CE=4.
由∵AB:BC=EF:CE=$\sqrt{3}$:1
∴EF=4$\sqrt{3}$
则,FH=EF-HE=EF-AB=4$\sqrt{3}$-2$\sqrt{3}$=2$\sqrt{3}$
BE=BC+CE=2+4=6
AH=BE=6
∴AF=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.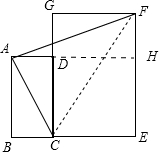
(2)证明:延长BM、EF相交于点P,
由题意知:AB∥EF,
∴∠ABM=∠P
∵点M是AF的中点,
∴AM=FM,
在△ABM和△FPM中
$\left\{\begin{array}{l}{∠ABM=∠P}&{(已证)}\\{∠PMF=∠BMA}&{(对顶角相等)}\\{AM=FM}&{(已证)}\end{array}\right.$
∴△ABM≌△FPM
∴BM=PM
又∵∠BEP=90°
∴EM=$\frac{1}{2}$BP=BM=PM
∵AB:BC=$\sqrt{3}$:1且AC=CE
∴AC=$\sqrt{B{C}^{2}+(\sqrt{3}BC)^{2}}$=2BC=CE
∴EP=$\sqrt{3}$BE
∴BP=$\sqrt{B{E}^{2}+(\sqrt{3}BE)^{2}}$=2BE
∴∠P=30°
又∵四边形CEFG是矩形
∴∠MBE=90°
∴∠BME=180°-30°=60°
∴△BEM是等边三角形(有一个角是60°的等腰三角形是等边三角形).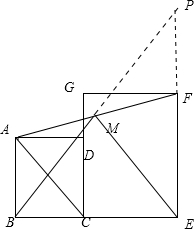
(3)(3)如图,连接AC、CF、取AC中点H,XF中点J,连接HB、HM、JE、JM.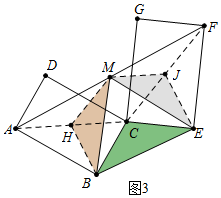
易证△BCH,△CJE是等边三角形,MJ=CH=BC,HM=JE=CE,
∵MJ∥AB,
∴∠MJC+∠ACJ=180°,
∵∠CJE=∠JCE=∠ACB=60°,
∴∠MJE+∠ACJ+120°=360°,
∵∠BCE+120°+∠ACJ=360°,
∴∠MJE=∠BCE,同理可证∠BHM=∠BCE,
∴△BCE≌△BHM≌△MJE,
∴BE=MB=BE,
故答案为△MBE是等边三角形.
点评 本题是四边形综合题,综合性强,属于运动开放性题目,考查了矩形性质、直角三角形的性质及勾股定理、旋转等多个知识点,关键是根据题目的结论去分析所需要的条件,从而根据图形特点及题目条件进行求解,特别问题(3),要开放思路利用数形结合的思想把一个几何问题应用代数的方法来解决.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
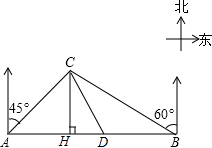 川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 由这两个统计图不能确定喜欢”小说”的人数 | |
| B. | 若该年级共有1200名学生,则可估计喜爱“科普常识”的学生有360人 | |
| C. | 由这两个统计图可知喜好“科普常识”的学生有90人 | |
| D. | 在扇形统计图中,“漫画”所在扇形的圆心角为72° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个平面直角坐标系,已知点A,B,C,D的坐标分别为(-2,-3),(2,-2),(3,1),(-4,5)按要求完成下列各小题.
如图是一个平面直角坐标系,已知点A,B,C,D的坐标分别为(-2,-3),(2,-2),(3,1),(-4,5)按要求完成下列各小题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com