
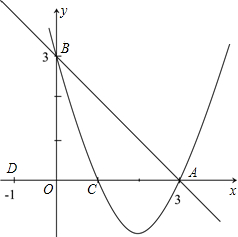
 如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.
如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.分析 (1)首先确定A、B、C三点的坐标,然后利用待定系数法求抛物线的解析式;
(2)△ABO为等腰直角三角形,若△ADP与之相似,则有两种情形,如答图1所示.利用相似三角形的性质分别求解,避免遗漏;
(3)如答图2所示,分别计算△ADE的面积与四边形APCE的面积,得到面积的表达式.利用面积的相等关系得到一元二次方程,将点E是否存在的问题转化为一元二次方程是否有实数根的问题,从而解决问题.需要注意根据(2)中P点的不同位置分别进行计算,在这两种情况下,一元二次方程的判别式均小于0,即所求的E点均不存在.
解答 解:(1)由题意得,A(3,0),B(0,3).
∵抛物线经过A、B、C三点,
∴把A(3,0),B(0,3),C(1,0)三点分别代入y=ax2+bx+c,
得方程组$\left\{\begin{array}{l}{9a+3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$
∴抛物线的解析式为y=x2-4x+3;
(2)由题意可得:△ABO为等腰三角形,如答图1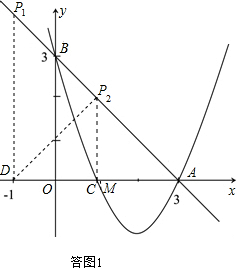 所示,
所示,
若△ABO∽△AP1D,则$\frac{AO}{AD}$=$\frac{OB}{D{P}_{1}}$,
∴DP1=AD=4,
∴P1(-1,4).
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,
∵△ABO为等腰三角形,
∴△ADP2是等腰三角形,
由三线合一可得:DM=AM=2=P2M,即点M与点C重合,
∴P2(1,2),
综上所述,点P的坐标为P1(-1,4),P2(1,2);
(3)不存在.
理由:如答图2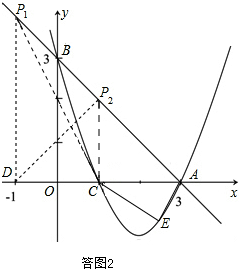 ,
,
设点E(x,y),则 S△ADE=$\frac{1}{2}$•AD•|y|=2|y|.
①当P1(-1,4)时,S四边形AP1CE=S△ACP1+S△ACE=$\frac{1}{2}$×2×4+$\frac{1}{2}$×2|y|=4+|y|,
∵△ADE的面积等于四边形APCE的面积,
∴2|y|=4+|y|,
∴|y|=4
∵点E在x轴下方,
∴y=-4,代入得:x2-4x+3=-4,即x2-4x+7=0,
∵△=(-4)2-4×7=-12<0
∴此方程无解
②当P2(1,2)时,S四边形AP2CE=S△ACP2+S△ACE=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2•|y|=2+|y|,
∵△ADE的面积等于四边形APCE的面积,
∴2|y|=2+|y|,
∴|y|=2.
∵点E在x轴下方,
∴y=-2,代入得:x2-4x+3=-2,即x2-4x+5=0,
∵△=(-4)2-4×5=-4<0,
∴此方程无解.
综上所述,在x轴下方的抛物线上不存在这样的点E.
点评 本题重点考查了抛物线的相关性质、相似三角形的性质、图形面积的计算以及一元二次方程根的判别式,涉及的知识点较多.注意在(2)(3)问中,均有两种情形,需要分类讨论计算,避免漏解;(3)问中是否存在点E的问题,转化为一元二次方程实数根个数的问题,需要注意这种解题方法.作为中考压轴题,本题综合性强,难度较大,有利于提高学生的综合解题能力,是一道不错的题目.


科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )
如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )| A. | (4$\sqrt{2}$,-4$\sqrt{2}$) | B. | (-4$\sqrt{2}$,4$\sqrt{2}$) | C. | (-8$\sqrt{2}$,8$\sqrt{2}$) | D. | (30,30) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
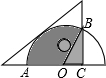 将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.
将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5.
如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.
如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com