
分析 (1)令x=0求出y的值,即可得到点A的坐标,求出对称轴解析式,即可得到点B的坐标;求出点A关于对称轴的对称点(2,-2),然后设直线l的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式解答即可;
(2)根据二次函数的对称性判断在2<x<3这一段与在-1<x<0这一段关于对称轴对称,然后判断出抛物线与直线l的交点的横坐标为-1,代入直线l求出交点坐标,然后代入抛物线求出m的值即可得到抛物线解析式.
解答 解:(1)当x=0时y=-2
所以A(0,-2)
抛物线对称轴为x=1,
所以B(1,0),
易得A点关于对称轴的对称点为A′(2,-2),
则直线经过A,B,
设直线的解析式为y=kx+b,
联立2k+b=-2与 k+b=0,
解得k=-2,b=2,
所以直线的解析式为y=-x+2;
(2)因为抛物线对称轴为x=1
所以抛物线在2<x<3这一段与在-1<x<0这一关于对称轴对称.
可观察到抛物线在-2<x<-1这一段在直线的上方,在-1<x<0这一段在直线的下方,
所以抛物线与直线的交点的横坐标为-1,
当x=-1时y=-2×(-1)+2=4,
则抛物线过点(-1,4),
当x=-1时,m+2m-2=4,m=2,
所以抛物线解析式为y=2x2-4x-2.
点评 本题考查了二次函数的性质,一次函数图象与几何变换,二次函数图象上点的坐标特征,根据二次函数的对称性求出抛物线经过的点(-1,4)是解题的关键.


科目:初中数学 来源: 题型:解答题
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5-$\frac{x}{5}$ |
| 捕捞量(kg) | 950-10x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
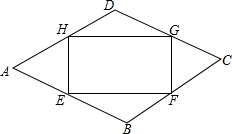 某公园要在菱形场地ABCD内划出一个矩形活动场地EFGH,要求矩形的四个顶点E、F、G、H分别在菱形场地的四条边上,且BE=BF=DG=DH菱形的周长为4am,∠ADC=120°.
某公园要在菱形场地ABCD内划出一个矩形活动场地EFGH,要求矩形的四个顶点E、F、G、H分别在菱形场地的四条边上,且BE=BF=DG=DH菱形的周长为4am,∠ADC=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=0,b=1 | B. | a=1,b=0 | C. | a=0,b=0 | D. | a=1,b=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com