
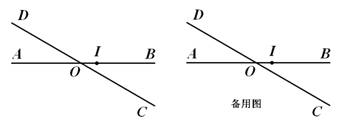
平面上两条直线AB、CD相交于点O,且∠BOD=1500(如图),现按如下要求规定此平面上点的“距离坐标”:
(1)点O的“距离坐标”为(0,0);
(2)在直线CD上,且到直线AB的距离为p(p>0)的点的“距离坐标”为(p,0);在直线AB上,且到直线CD的距离为q(q>0)的点的“距离坐标”为(0,q);
(3)到直线AB、CD的距离分别为p、q(p>0,q>0)的点的“距离坐标”为(p,q)。
设M为此平面上的点,其“距离坐标”为(m,n),根据上述对点的“距离坐标”的规定,解决下列问题:
(1)画出图形(保留画图痕迹):
①满足m=1且n=0的点的集合;
②满足m=n的点的集合;
(2)若点M在过点O且与直线CD垂直的直线l上,求m与n所满足的关系式。
(说明:图中OI长为一个单位长)
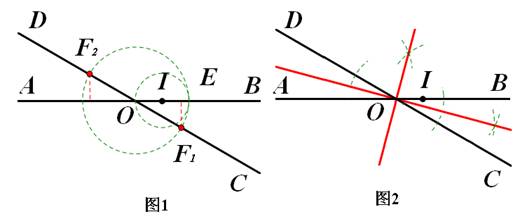
(1)①如图1中,F1,F2即为所求;②如图2中,两条角平分线即为所求
(2)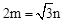
【解析】解:(1)①如图1中,F1,F2即为所求;
②如图2中,两条角平分线即为所求。
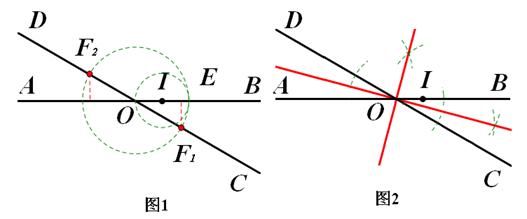
(2)如图3,过点M作MH⊥AB于点H。
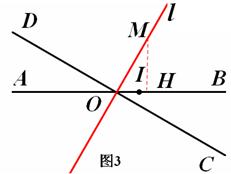
则根据定义,MH=m,MO=n。
∵∠BOD=1500,∠DOM=900(∵l⊥CD),
∴ ∠HOM=600。
在Rt△MHO中, ,
,
∴ 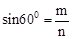 ,即
,即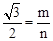 ,即
,即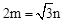
∴ m与n所满足的关系式为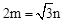 。
。
(1)①以点I为圆心,OI为半径画圆交AB于点E;以点O为圆心,OE为半径画圆交CD于点F1,F2,则F1,F2即为所求。
由作法知,OF1=2OI=2,由∠BOD=1500知∠EOF1=300,根据含300角直角三角形中300角所对边是斜边一半的性质,得点F1到AB的距离m =1,同时点F1在CD上,即n=0。同理,F2的证明。
②分别作∠BOD和∠BOC的平分线,根据角平分线上的点到角的两边距离相等的性质,两角平分线上的点满足m=n,故两条角平分线即为所求。
(2)由已知和锐角三角函数定义即可得出m与n所满足的关系式。


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏常州卷)数学(带解析) 题型:解答题
平面上两条直线AB、CD相交于点O,且∠BOD=1500(如图),现按如下要求规定此平面上点的“距离坐标”:
(1)点O的“距离坐标”为(0,0);
(2)在直线CD上,且到直线AB的距离为p(p>0)的点的“距离坐标”为(p,0);在直线AB上,且到直线CD的距离为q(q>0)的点的“距离坐标”为(0,q);
(3)到直线AB、CD的距离分别为p、q(p>0,q>0)的点的“距离坐标”为(p,q)。
设M为此平面上的点,其“距离坐标”为(m,n),根据上述对点的“距离坐标”的规定,解决下列问题:
(1)画出图形(保留画图痕迹):
①满足m=1且n=0的点的集合;
②满足m=n的点的集合;
(2)若点M在过点O且与直线CD垂直的直线l上,求m与n所满足的关系式。
(说明:图中OI长为一个单位长)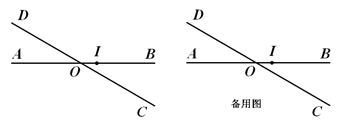
查看答案和解析>>
科目:初中数学 来源:江苏中考真题 题型:解答题
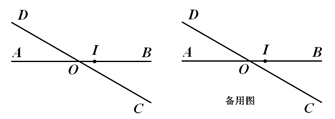
查看答案和解析>>
科目:初中数学 来源: 题型:
平面上两条直线AB、CD相交于点O,且∠BOD=1500(如图),现按如下要求规定此平面上点的“距离坐标”:
(1)点O的“距离坐标”为(0,0);
(2)在直线CD上,且到直线AB的距离为p(p>0)的点的“距离坐标”为(p,0);在直线AB上,且到直线CD的距离为q(q>0)的点的“距离坐标”为(0,q);
(3)到直线AB、CD的距离分别为p、q(p>0,q>0)的点的“距离坐标”为(p,q)。
设M为此平面上的点,其“距离坐标”为(m,n),根据上述对点的“距离坐标”的规定,解决下列问题:
(1)画出图形(保留画图痕迹):
①满足m=1且n=0的点的集合;
②满足m=n的点的集合;
(2)若点M在过点O且与直线CD垂直的直线l上,求m与n所满足的关系式。
(说明:图中OI长为一个单位长)
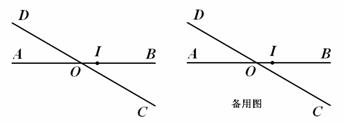
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com