
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 7 |
| 4 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 7 |
| 11 |
| 7 |
| 11 |
| 4 |
| 11 |
| 4 |
| 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:
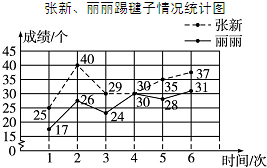 体育老师要从每班选取一名同学,参加学校的秋季趣味运动会的踢毽子项目比赛.七年级二班张新和丽丽是踢毽子健将,下面是张新、丽丽几次踢毽子情况的统计图:
体育老师要从每班选取一名同学,参加学校的秋季趣味运动会的踢毽子项目比赛.七年级二班张新和丽丽是踢毽子健将,下面是张新、丽丽几次踢毽子情况的统计图:查看答案和解析>>
科目:初中数学 来源: 题型:
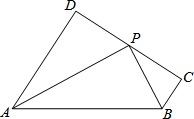 如图,AD∥BC,∠DAB的平分线与∠CBA的平分线交于点P,过点P的直线垂直于AD,垂足为D,交BC于点C.试问:点P是线段CD的中点吗?为什么?
如图,AD∥BC,∠DAB的平分线与∠CBA的平分线交于点P,过点P的直线垂直于AD,垂足为D,交BC于点C.试问:点P是线段CD的中点吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com