
分析 通过观察前8个数据,可以得出规律,这些数字7个一个循环,根据这些规律计算即可.
解答 解:(1)F2(4)=F(F1(4))=F(16)=12+62=37;
F1(4)=F(4)=16,F2(4)=37,F3(4)=58,
F4(4)=89,F5(4)=145,F6(4)=26,F7(4)=40,F8(4)=16,
通过观察发现,这些数字7个一个循环,2015是7的287倍余6,因此F2015(4)=26;
(2)由(1)知,这些数字7个一个循环,F4(4)=89=F18(4),因此3m=18,所以m=6.
故答案为:(1)37,26;(2)6.
点评 本题属于数字变化类的规律探究题,通过观察前几个数据可以得出规律,熟练找出变化规律是解题的关键.


科目:初中数学 来源: 题型:解答题
 已知,如图,在△ABC中和△A′B′C′中,∠BAC=∠B′A′C′,AB=A′B′,AD和A′D′分别是△ABC和△A′B′C′的角平分线,且AD=A′D′,求证:△ABC≌△A′B′C′.
已知,如图,在△ABC中和△A′B′C′中,∠BAC=∠B′A′C′,AB=A′B′,AD和A′D′分别是△ABC和△A′B′C′的角平分线,且AD=A′D′,求证:△ABC≌△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2-16=(m+4)(m-4) | B. | m2+3m+9=(m+3)2 | C. | m2-8m+16=(m-4)2 | D. | m2+4m=m(m+4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
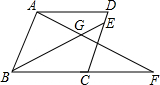 如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?
如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com