
 如图,已知点O为平行四边形ABCD所在平面上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,求$\overrightarrow{OD}$(用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,已知点O为平行四边形ABCD所在平面上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,求$\overrightarrow{OD}$(用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示) 分析 根据平行四边形的性质得到AB∥CD且AB=CD,结合三角形法则进行解答.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD且AB=CD,
∵$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,
∴$\overrightarrow{BA}$=$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{a}$-$\overrightarrow{b}$,
∴$\overrightarrow{CD}$=$\overrightarrow{BA}$=$\overrightarrow{a}$-$\overrightarrow{b}$,
又$\overrightarrow{OC}$=$\overrightarrow{c}$,
∴$\overrightarrow{OD}$=$\overrightarrow{OC}$+$\overrightarrow{CD}$=$\overrightarrow{c}$+$\overrightarrow{a}$-$\overrightarrow{b}$.
点评 本题考查了平行四边形的性质和平面向量,掌握三角形法则是解题的关键.


科目:初中数学 来源: 题型:解答题
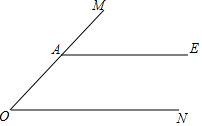 如图,A是∠MON边OM上一点,AE∥ON.
如图,A是∠MON边OM上一点,AE∥ON.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 星期天的早晨,小明骑自行车从家出发,到离家1050米的书店买书,出发1分钟后,他到达离家150米的地方,又过1分钟后,小明加快了速度.如图所示是小明从家出发后离家的路程y(米)与他骑自行车的时间x(分钟)之间的函数图象.根据图象解答下列问题:
星期天的早晨,小明骑自行车从家出发,到离家1050米的书店买书,出发1分钟后,他到达离家150米的地方,又过1分钟后,小明加快了速度.如图所示是小明从家出发后离家的路程y(米)与他骑自行车的时间x(分钟)之间的函数图象.根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
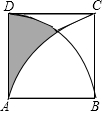 如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.
如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}$≤m≤4$\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
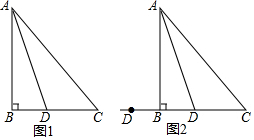 在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.
在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径r=2,扇形圆心角θ=120°,则该圆锥母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径r=2,扇形圆心角θ=120°,则该圆锥母线长为( )| A. | 10 | B. | $\frac{15}{2}$ | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com