
分析 (1)根据分式的乘法法则进行计算即可.
(2)根据分式的乘法和除法法则进行计算.
(3)根据分式的乘法和除法法则进行计算.
(4)根据分式的乘法和除法法则进行计算.其中注意能因式分解的要进行因式分解.
(5)根据分式的乘法和除法法则进行计算.其中注意能因式分解的要进行因式分解.
(6)根据分式的乘法和除法法则进行计算.其中注意能因式分解的要进行因式分解.
解答 解:(1)($\frac{-3{x}^{2}y}{9{z}^{2}}$)2
=$(\frac{-3{x}^{2}y}{9{z}^{2}})(\frac{-3{x}^{2}y}{9{z}^{2}})$
=$\frac{9{x}^{4}{y}^{2}}{81{z}^{4}}$
=$\frac{{x}^{4}{y}^{2}}{9{z}^{4}}$.
(2)$\frac{4{a}^{2}b}{3c{d}^{2}}$•$\frac{5{c}^{2}d}{4a{b}^{2}}$÷$\frac{2abc}{3d}$
=$\frac{4{a}^{2}b}{3c{d}^{2}}•\frac{5{c}^{2}d}{4a{b}^{2}}•\frac{3d}{2abc}$
=$\frac{5}{2{b}^{2}}$.
(3)($\frac{-a}{b}$)2÷($\frac{2{a}^{2}}{5b}$)2•$\frac{a}{5b}$
=$\frac{{a}^{2}}{{b}^{2}}•\frac{25{b}^{2}}{4{a}^{4}}•\frac{a}{5b}$
=$\frac{5}{4ab}$.
(4)$\frac{81-{a}^{2}}{{a}^{2}+6a+9}$÷$\frac{a-9}{2a+6}$•$\frac{a+3}{a+9}$
=$\frac{(9+a)(9-a)}{(a+3)^{2}}×\frac{2(a+3)}{(a-9)}•\frac{a+3}{a+9}$
=-2.
(5)$\frac{2x-6}{4-4x+{x}^{2}}$÷(x+3)•$\frac{(x+3)(x-2)}{3-x}$
=$\frac{2(x-3)}{(x-2)^{2}}×\frac{1}{x+3}•\frac{(x+3)(x-2)}{3-x}$
=$\frac{2}{2-x}$.
(6)($\frac{5xy}{{x}^{3}-{x}^{2}y}$)2•(-$\frac{{x}^{2}y}{5}$)2•($\frac{1}{x}$-$\frac{1}{y}$)3
=$(\frac{5y}{{x}^{2}-xy})^{2}•\frac{{x}^{4}{y}^{2}}{25}•(\frac{y-x}{xy})^{3}$
=$\frac{25{y}^{2}}{{x}^{2}(x-y)^{2}}•\frac{{x}^{4}{y}^{2}}{25}•\frac{(y-x)^{3}}{{x}^{3}{y}^{3}}$
=$\frac{-y(x-y)}{x}$
=$\frac{{y}^{2}-xy}{x}$.
点评 本题主要考察分式的乘法和除法法则,其中关键是要将能因式分解的要进行因式分解,在乘除过程中可以进行约分化简,使问题简单化,要注意将结果化到最简.


科目:初中数学 来源: 题型:解答题
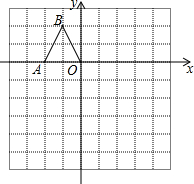 如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
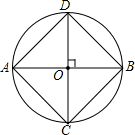 如图,AB、CD是⊙O的两条互相垂直的直径.
如图,AB、CD是⊙O的两条互相垂直的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-4(x+3)2-2 | B. | y=-4(x+3)2+2 | C. | y=-4(x-3)2-2 | D. | y=-4(x-3)2+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com