
 如图,在四边形ABCD中,∠A=90°,AD∥BC,E为AB的中点,连接CE,BD,过点E作FE⊥CE于点E,交AD于点F,连接CF,已知2AD=AB=BC.
如图,在四边形ABCD中,∠A=90°,AD∥BC,E为AB的中点,连接CE,BD,过点E作FE⊥CE于点E,交AD于点F,连接CF,已知2AD=AB=BC.分析 (1)由E为AB的中点,得到AB=2BE,等量代换得到BE=AD,推出△ABD≌△BCE,根据全等三角形的性质即可得到结论;
(2)根据已知条件得到AE=BE=2,BC=4,根据余角的性质得到∠AFE=∠BEC,根据相似三角形的性质即可得到结论;
(3)根据相似三角形的性质得到AF=$\frac{1}{2}$AE,设AF=k,则AE=BE=2k,BC=4k,根据勾股定理得到EF=$\sqrt{5}$k,CE=2$\sqrt{5}$k,CF=5k,由三角函数的定义即可得到结论.
解答 解:(1)∵E为AB的中点,
∴AB=2BE,
∵AB=2AD,
∴BE=AD,
∵∠A=90°,AD∥BC,
∴∠ABC=90°,
在△ABD与△BCE中,$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠ABC}\\{AD=BE}\end{array}\right.$,
∴△ABD≌△BCE,
∴CE=BD;
(2)∵AB=4,
∴AE=BE=2,BC=4,
∵FE⊥CE,
∴∠FEC=90°,
∴∠AEF+∠AFE=∠AEF+∠BEC=90°,
∴∠AFE=∠BEC,
∴△AEF∽△BCE,
∴$\frac{AF}{BE}=\frac{AE}{BC}$,
∴AF=1;
(3)∵△AEF∽△BCE,
∴$\frac{AF}{BE}=\frac{AE}{BC}$,
∴AF=$\frac{1}{2}$AE,
设AF=k,则AE=BE=2k,BC=4k,
∴EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{5}$k,
CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=2$\sqrt{5}$k,
∴CF=$\sqrt{E{F}^{2}+C{E}^{2}}$=5k,
∴sin∠EFC=$\frac{CE}{CF}$=$\frac{2\sqrt{5}}{5}$.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
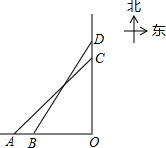 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,此时测得轮船乙在甲的东北方向,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,此时测得轮船乙在甲的北偏东32°,此时B处距离码头O多远?(结果保留一位小数)(参考数据:sin32°≈0.53,cos32°≈0.85,tan58°≈1.60,tan32°≈0.625)
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,此时测得轮船乙在甲的东北方向,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,此时测得轮船乙在甲的北偏东32°,此时B处距离码头O多远?(结果保留一位小数)(参考数据:sin32°≈0.53,cos32°≈0.85,tan58°≈1.60,tan32°≈0.625)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
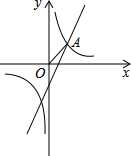 如图,己知点A是反比例函数y=$\frac{1}{x}$的图象与一次函数y=2x-1的图象在第一象限的交点,点P是x轴上一点,当△OAP为等腰三角形时,点P的坐标为($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).
如图,己知点A是反比例函数y=$\frac{1}{x}$的图象与一次函数y=2x-1的图象在第一象限的交点,点P是x轴上一点,当△OAP为等腰三角形时,点P的坐标为($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 16.5 | C. | 17 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com