练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】初三年级261位学生参加期末考试，某班35位学生的语文成绩、数学成绩与总成绩在全年级中排名情况如图1和图2所示，甲、乙、丙为该班三位学生.

    从这次考试成绩看，①在甲、乙两人中，总成绩名次靠前的学生是______；

    ②在语文和数学两个科目中，丙同学的成绩名次更靠前的科目是______.

    你选择的理由是____________.

    【答案】甲 数学 丙这个点的位置比右边图中丙的位置高,所以语文名次更“大”,即在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是数学.

    【解析】

    (1)根据图1分析甲乙两人所在的位置的横坐标即可确定总成绩名次

    (2)根据图2分析丙所在位置的横坐标,确定丙的总成绩年级名次是倒数第5,在图1中找出从右数第5个点即为丙的位置,观察图1和图2中丙的纵坐标即可得出答案

    (1)由图1可知甲的位置在乙的左侧,所以在甲、乙两人中,总成绩名次靠前的学生是甲；

    (2)由初三年级261位学生参加期末考试,某班35位学生的语文成绩,数学成绩与总成绩在全年级的排名情况图可知,两个图中,同一个人的总成绩是不会变的.从图2看,丙是从右往左数第5个点,即丙的总成绩在班里倒数第5.在图1中,找到倒数第5个点,它表示的就是丙,发现这个点的位置比右边图中丙的位置高,所以语文名次更“大”,即在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是数学；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为的正方形四个角上，分别剪去大小相等的等腰直角三角形，当三角形的直角边由小变大时，阴影部分的面积也随之发生变化，它们的变化情况如下：

    三角形的直角边长/

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    阴影部分的面积/

    398

    392

    382

    368

    350

    302

    272

    200

    （1）在这个变化过程中，自变量、因变量各是什么？

    （2）请将上述表格补充完整；

    （3）当等腰直角三角形的直角边长由增加到时，阴影部分的面积是怎样变化的？

    （4）设等腰直角三角形的直角边长为，图中阴影部分的面积为，写出与的关系式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，y轴上有一点A（0，1），点B是x轴上一点，∠ABO＝60°，抛物线y＝﹣x2++3与x轴交于C、D两点（点C在点D的左侧）．

    （1）将点C向右平移个单位得到点E，过点E作直线l⊥x轴，点P为y轴上一动点，过点P作PQ⊥y轴交直线l于点Q，点K为抛物线上第一象限内的一个动点，当△ABK面积最大时，求KQ+QP+PE的最小值，及此时点P的坐标；

    （2）在（1）的条件下，将线段PE绕点P逆时针旋转90°后得线段PE′，问：在第一象限内是否存在点S，使得△SPE'是有一个角为60°，且以线段PE′为斜边的直角三角形，若存在请直接写出所有满足条件的点S，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,四边形ABCD中,∠ABC、∠ADC的平分线分別交CD、AB上点E、F.

    (1)若∠ABC=∠ADC,求征:∠ADF=∠ABE;

    (2)如图，若∠A与∠C互朴，试探究∠ADF与∠ABE之同的数量夫系，并说明理由;

    (3)如图,在(2)的条件下，当DA⊥AB时，试探究BE与DF的位置关系，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图，在中，是高，是角平分线，当，，则____；

    （2）若和的度数分别用字母和来表示（），你能找到与和之间的关系吗？ ______.（请直接写出你发现的结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）阅读下面的材料并把解答过程补充完整.

    问题：在关于，的二元一次方程组中，，，求的取值范围.

    在关于，的二元一次方程组中，利用参数的代数式表示，，然后根据，列出关于参数的不等式组即可求得的取值范围.解：由，解得，又因为，，所以解得____________.

    （2）请你按照上述方法，完成下列问题：

    ①已知，且，，求的取值范围；

    ②已知，在关于，的二元一次方程组中，，，请直接写出的取值范围（结果用含的式子表示）____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B，有人在直线AB上点C（靠点B一侧）竖直向上摆放若干个无盖的圆柱形桶．试图让网球落入桶内，已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．当竖直摆放圆柱形桶至少________个时，网球可以落入桶内．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

    （1）求证：AF=DC；

    （2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

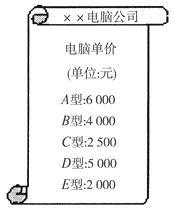
    【题目】如图，某电脑公司现有A，B，C三种型号的甲品牌电脑和D，E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.

    (1)写出所有选购方案(利用树状图或列表方法表示）；

    (2)如果(1)中各种选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？

    (3)现知希望中学用10万元购买甲、乙两种品牌电脑共36台(价格如图所示)，其中甲品牌电脑为A型号电脑，求购买的A型号电脑有多少台？

    查看答案和解析>>

    同步练习册答案