
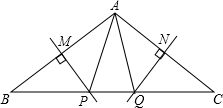
 如图所示,MP和 NQ分别垂直平分AB 和AC.
如图所示,MP和 NQ分别垂直平分AB 和AC.分析 (1)先根据三角形内角和等于180°求出∠ABP+∠ACQ=75°,再根据线段垂直平分线的性质∠PAB=∠ABP,∠QAC=∠ACQ,所以∠PAB+∠QAC=75°,便不难求出∠PAQ的度数为30°;
(2)根据线段垂直平分线的性质,得AP=BP,AQ=CQ,则∠B=∠BAP,∠C=∠CAQ,则∠APQ=2∠B,∠AQP=2∠C;根据三角形的内角和定理,得∠APQ+∠AQP=180°-∠PAQ=150°,则∠B+∠C=75°,进而求解.
解答 解:(1)∵∠BAC=105°,
∴∠ABP+∠ACQ=180°-105°=75°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=75°,
∴∠PAQ=105°-75°=30°;
(2)∵MP和NQ分别垂直平分AB和AC,
∴AP=BP,AQ=CQ,
∴∠B=∠BAP,∠C=∠CAQ,
∴∠APQ=2∠B,∠AQP=2∠C.
∵∠PAQ=25°,
∴∠APQ+∠AQP=180°-∠PAQ=155°,
∴∠B+∠C=77.5°.
∴∠BAC=∠B+∠C+∠PAQ=77.5°+25°=102.5°.
点评 此题综合运用了线段垂直平分线的性质、等腰三角形的性质以及三角形的外角的性质.


科目:初中数学 来源: 题型:解答题
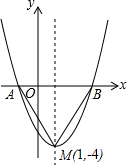 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3或12 | B. | 12或27 | C. | 40或8 | D. | 3或12或27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
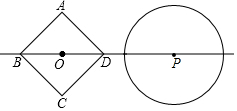 如图,正方形ABCD的边长为$\sqrt{2}$,⊙P的半径为1,正方形ABCD的中心O和⊙P的圆心P都在直线l上,线段OP的长叫做它们的中心距,⊙P随着点P在直线l上的运动而运动.
如图,正方形ABCD的边长为$\sqrt{2}$,⊙P的半径为1,正方形ABCD的中心O和⊙P的圆心P都在直线l上,线段OP的长叫做它们的中心距,⊙P随着点P在直线l上的运动而运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>0,b>0,则a+b>0 | B. | 若a<0,b<0,则a-b<0 | ||
| C. | 若a>0,b<0,且|a|>|b|,则a-b>0 | D. | 若a<0,b>0,且|a|>|b|,则a-b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
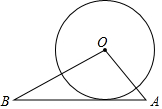 如图,在△OAB中,OA=2$\sqrt{5}$,OB=4$\sqrt{5}$,OA⊥OB,以O为圆心,4为半径作⊙O,求证:AB是⊙O的切线.
如图,在△OAB中,OA=2$\sqrt{5}$,OB=4$\sqrt{5}$,OA⊥OB,以O为圆心,4为半径作⊙O,求证:AB是⊙O的切线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com