
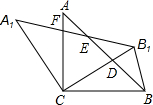
 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设B1C交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设B1C交AB于D,A1B1分别交AB,AC于E,F分析 (1)根据已知条件,利用旋转的性质及全等三角形的判定方法,来判定三角形全等.
(2)当△BBD是等腰三角形时,要分别讨论B1B=B1D、BB1=BD、B1D=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
解答 解:(1)△CBD≌△CA1F,
∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,
∵$\left\{\begin{array}{l}{∠CBD=∠C{A}_{1}F}\\{BC={A}_{1}F}\\{∠BCD=∠{A}_{1}CF}\end{array}\right.$,
∴△CBD≌△CA1F(ASA).
(2)在△CBB1中,∵CB=CB1
∴∠CBB1=∠CB1B=$\frac{1}{2}$(180°-α).
又∵△ABC是等腰直角三角形,
∴∠ABC=45°.
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,∠B1BD=∠CBB1-45°=$\frac{1}{2}$(180°-α)-45°=45°-$\frac{α}{2}$,
∴45°+α=45°-$\frac{α}{2}$,
∴α=0°(舍去);
②∵∠BB1C=∠B1BC>∠B1BD,
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,
即45°+α=$\frac{1}{2}$(180°-α),
解得:α=30°
综上,当△BB1D为等腰三角形时,α=30°.
点评 本题考查旋转的性质、三角形全等的判定与性质、等腰三角形的判定与性质等知识点,根据△BB1D是等腰三角形分类讨论是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
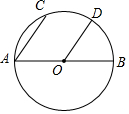 如图,AB是⊙O的直径,OD∥AC,C,D两点均在⊙O上,则$\widehat{CD}$与$\widehat{BD}$有何大小关系?为什么?
如图,AB是⊙O的直径,OD∥AC,C,D两点均在⊙O上,则$\widehat{CD}$与$\widehat{BD}$有何大小关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
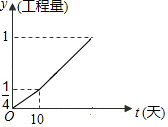 甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程,设工程总量为1,后期总工程量y与天数t之间的关系为y=kx-$\frac{1}{6}$,若工程进度如图所示,则实际完成这项工程所用的时间比甲单独完成此项工作所用的时间少12天.
甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程,设工程总量为1,后期总工程量y与天数t之间的关系为y=kx-$\frac{1}{6}$,若工程进度如图所示,则实际完成这项工程所用的时间比甲单独完成此项工作所用的时间少12天.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com