Question

 

1.探究新知

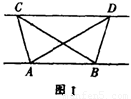
如图1，已知ΔABC与ΔABD的面积相等，试判断AB与CD的位置关系，并说明理由；[来源:

2.结论应用：

如图2，过点M，N在反比例函数的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F。试证明MN//EF。

 

Answer 1

 

1.分别过点C、D作CG⊥AB，DH⊥AB，垂足为GH，则

∴CG//DH，

∵ΔABG与ΔABD的面积相等，

∵CG=DH    …………………………………………………………………………3分

∴四边形CGHD为平行四边形，

∴AB//CD。………………………………………………………………………………5分

2.证明：连接MF，NE，设点M的坐标为（x₁，y₁），点N的坐标为（x₂，y₂）。

∵点M、N在反比例函数的图象上，

∵x₁y₁=k，x₁y₂=k。……………………………………………………………………7分

∵ME⊥y轴，NF⊥x轴，

∴OE=y₁，OF=x₂，

∴。……………………………………………………………8分

，

，

由（1）中的结论可知MN//EF。………………………………………………………10分

解析:根据同底等高的三角形面积相等，得出两个三角形的高相等，从而得出两直线平行；设出M、N两点坐标，表示出△EFM和△EFN的面积，利用反比例函数的性质得两三角形面积相等.利用（1）的结论得出两直线平行.