
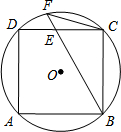
 如图,⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,则弦FC的长为$\frac{\sqrt{10}}{5}$.
如图,⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,则弦FC的长为$\frac{\sqrt{10}}{5}$. 分析 连接BD,构造△DBE,然后证出△DBE∽△FCE,列出比例式计算FC即可.
解答 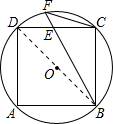 解:连接BD,
解:连接BD,
∵CE=$\frac{1}{2}$×1=$\frac{1}{2}$,
∴BE=$\sqrt{{(\frac{1}{2})}^{2}+1}$=$\frac{\sqrt{5}}{2}$,
在Rt△ABD中,BD=$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$,
∵∠DBE=∠FCE,∠CFE=∠BDE,
∴△DEB∽△FEC,
∴$\frac{FC}{BD}$=$\frac{CE}{BE}$,
∴$\frac{FC}{\sqrt{2}}$=$\frac{\frac{1}{2}}{\frac{\sqrt{5}}{2}}$,
∴FC=$\frac{\sqrt{10}}{5}$.
故答案为:$\frac{\sqrt{10}}{5}$.
点评 本题考查了正多边形和圆,相似三角形的判定和性质,作出适当辅助线,得到相似三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{3}$,则k的值为-6.
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{3}$,则k的值为-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
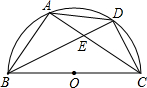 如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=$\sqrt{5}$,CD=2.
如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=$\sqrt{5}$,CD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
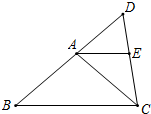 如图,在△ABC中,AB=AC=5cm,∠DCA=∠B,点D在BA延长线上,AE∥BC,交CD于点E,AE=$\frac{25}{8}$cm.
如图,在△ABC中,AB=AC=5cm,∠DCA=∠B,点D在BA延长线上,AE∥BC,交CD于点E,AE=$\frac{25}{8}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
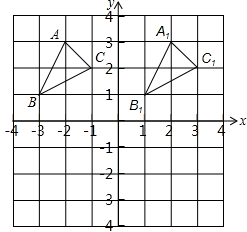 如图平面直角坐标系,在三角形ABC中,A(-2,3),B(-3,1),C(-1,2).
如图平面直角坐标系,在三角形ABC中,A(-2,3),B(-3,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2006 | B. | 1-20072 | C. | 1-20062 | D. | 123456 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com